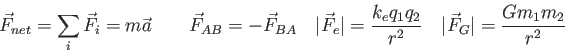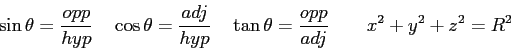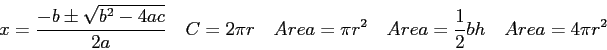Physics 131-01 Test 2


I pledge that I have neither given nor received unauthorized assistance during the completion of this work.


Signature height0pt depth1pt width3in


Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

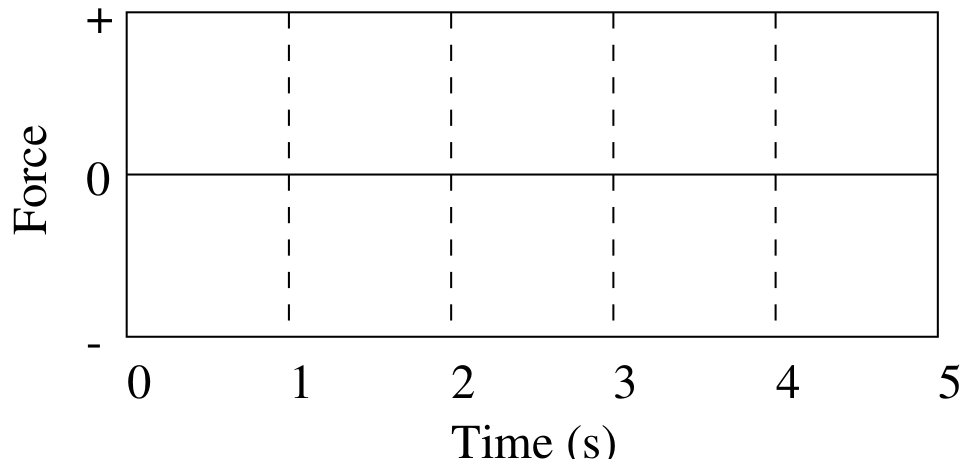
  1. The first figure below shows an object's velocity-time graph as it moves along a horizontal line (the + position axis). Sketch the shape of the force graph on the other axes. Explain your reasoning.




    Image q1fig2

  2. Can a flexible force transmitter (like a string) support a lateral (or sideways) force? Explain your reasoning.









  3. Suppose somebody tosses you a raw egg and you catch it. Suppose the time you take to bring the egg to a stop is 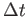$\Delta t$. Would you rather catch the egg in such a way that 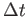$\Delta t$ is small or large? Why?








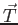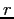  4. Consider the diagram of the airplane laboratory. Draw a complete free-body diagram of the forces acting on the airplane and write down Newton's Second Law for the components of the forces acting on the airplane in terms of the tension $\vec T$ in the string, the length $L$ of the string, the radius $r$ of the airplanes's orbit, the speed 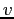$v$ of the airplane, and its mass $m$.




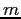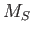  5. Consider an asteroid that gets captured by the planet Saturn inside the Roche limit $R_R = \sqrt[3]{(12 M_S)/(\pi \rho_{dirt})}$ where $M_S$ is Saturn's mass and 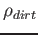$\rho_{dirt}$ is the density of dirt. In this region of space the tidal forces that create Roche's limit can tear the asteroid apart. Would that be more likely to happen if the asteroid were a solid chunk of rock (rigid-body model) or a collection of smaller pieces bound together by their mutual gravity (rubble-pile model)? Explain.









Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1. 15 pts. A football player of mass $m=110~kg$ is gliding across very smooth, frictionless ice at a speed $v_0 = 1.50~ m/s$ carrying a football of mass $m_b = 0.45~kg$ (unless you're Tom Brady). He throws the football straight forward. What is the player's speed afterward if the ball is thrown at a speed $v_b= 20~m/s$ relative to the ground?

2. 20 pts. Because the Earth rotates about its axis, a point on the equator experiences a centripetal acceleration of $a_e = 0.0337~m/s^2$ whereas a point at the poles experiences no centripetal acceleration. Assume the Earth is a uniform sphere with $g=9.800~m/s^2$.

a. Show that at the equator the gravitational force on an object must exceed the normal force required to support the object.
b. If a person at the equator has a mass $m=70~kg$ what is the gravitational force on the person?
c. What is the normal force on the person?

3. 25 pts. A block of mass $m= 10~kg$ is released from point A in the figure. The track is frictionless except for a rough surface in the region between points B and C of length $L=6~m$ where the block will lose some of its mechanical energy due to the work done by friction when it slides through. The block is released from rest and slides down the track, passes through the rough surface, and eventually hits the spring (force constant $k = 2.25\times 10^3~N/m$). The block compresses the spring a distance $x_s = 0.3~m$ from it's equilibrium position before momentarily coming to rest. What is the coefficient of kinetic friction between the block and the rough surface between points B and C?

Image p3f1

Physics 131-01 Equations and Constants



\begin{displaymath} \Delta \vec r = \vec r_{finish} - \vec r_{start} \quad \Delta \vec v = \vec v_{finish} - \vec v_{start} \end{displaymath}


\begin{displaymath} \langle \vec v \rangle = {\Delta \vec r \over \Delta t} \qqu... ...ta t \to 0} {\vec r (t+\Delta t) - \vec r(t) \over \Delta t} \end{displaymath}


\begin{displaymath} \langle \vec a \rangle = {\Delta \vec v \over \Delta t} \qqu... ...lta t \to 0} {\vec v(t+\Delta t) - \vec v(t) \over \Delta t} \end{displaymath}


\begin{displaymath} x(t) = {1 \over 2}at^2 + v_0t + y_0 \quad v = at + v_0 \quad... ...er r} \quad ( \vec v \perp \vec r \quad \vec v \perp \vec a_c) \end{displaymath}


\begin{displaymath} \vec F_{net} = \sum_i \vec F_i = m \vec a \qquad \vec F_{AB}... ...q_1 q_2}{r^2} \quad \vert\vec F_G\vert = \frac{G m_1 m_2}{r^2} \end{displaymath}


\begin{displaymath} \vert\vec F_k\vert = \mu_k N \quad \vert\vec F_s\vert \le \m... ...} \quad \vec F_s(x) = -kx\hat i \quad \vec F_g(y) = -mg\hat j \end{displaymath}


\begin{displaymath} W = \int \vec F \cdot d\vec s = \int \vert\vec F\vert \ver... ...ver 2} mv^2 \quad PE_g = mgh \quad PE_s = {1\over 2}kx^2 \quad \end{displaymath}


\begin{displaymath} ME = KE + PE \rightarrow ME_f = ME_i \quad %\rightarrow KE_f... ... \vec p \quad \vec p = m\vec v \rightarrow \vec p_i = \vec p_f \end{displaymath}


\begin{displaymath} \vec A = A_x \hat i + A_y \hat j + A_z \hat k \qquad {dA \ov... ... 0 \qquad {dt \over dt} = 1 \qquad {dt^2 \over dt} = 2t \qquad \end{displaymath}


\begin{displaymath} \int f(x)dx = \lim_{\Delta x \rightarrow 0} \sum f(x_i) \Delta x \qquad \end{displaymath}


\begin{displaymath} \sin \theta = {opp \over hyp} \quad \cos \theta = {adj \over... ...uad \tan \theta = {opp \over adj} \qquad x^2 + y^2 + z^2 = R^2 \end{displaymath}


\begin{displaymath} x = {-b \pm \sqrt{b^2 -4ac} \over 2a} \quad C = 2 \pi r \qua... ...pi r^2 \quad Area = {1 \over 2}bh \quad Area = 4 \pi r^2 \quad \end{displaymath}


\begin{displaymath} V = {4 \over 3}\pi r^3 \quad V = \pi r^2 l \quad \theta = {s \over r} \quad \rho = {m \over V} \end{displaymath}

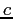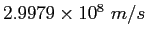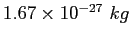Speed of Light ($c$) $2.9979\times 10^8 m/s$ proton/neutron mass $1.67\times 10^{-27} kg$
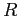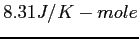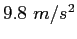$R$ $8.31J/K-mole$ $g$ $9.8 m/s^2$
Gravitation constant 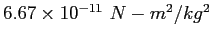$6.67 \times 10^{-11} N-m^2/kg^2$ Earth's radius $6.37\times 10^6 m$
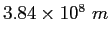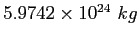Earth-Moon distance $3.84\times 10^8 m$ Earth mass $5.9742\times 10^{24} kg$
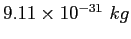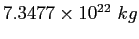Electron mass $9.11\times 10^{-31} kg$ Moon mass $7.3477\times 10^{22} kg$