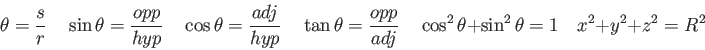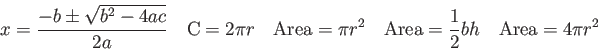Physics 131-01 Test 1
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
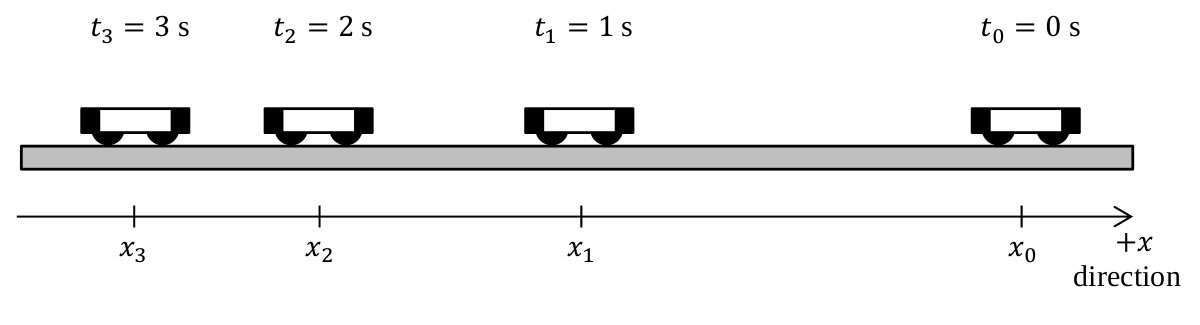
- At each indicated time on the figure below,
sketch, and label,
a vector above the cart which might represent the velocity of the cart at that
time while it is moving toward the motion detector and slowing down.
Show how you would find the vector representing the change in velocity
between the times 2 s and 3 s using those vectors.
What is the sign of the acceleration?
Clearly state the vector equations you are applying.
- For our study of toy airplanes flying in circles, how are the position vector and velocity vector related?
What is your evidence?
- What advantages do histograms have over just calculating the average and standard deviation?
- The plot below shows the results of a student's analysis of
the
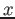 component of projectile motion with Tracker.
They ask you if it looks right. What do you answer? Explain.
component of projectile motion with Tracker.
They ask you if it looks right. What do you answer? Explain.
- While riding in a moving car, you toss an egg directly upward.
Does the egg land behind you, in front of you, or back in your hands if the car
is decreasing in speed? Explain.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
Note: Derivatives should be
calculated using the the definition in terms of a limit.
| 1. |
15 pts. |
A particle's velocity is described by the function
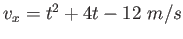 , where , where 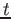 is in seconds.
At what times does the particle reach its turning points? is in seconds.
At what times does the particle reach its turning points?
|
| 2. |
20 pts. |
A rifle is aimed horizontally at a target a distance  away.
The bullet hits the target a distance away.
The bullet hits the target a distance 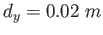 below the aim point.
What was the bullet's flight time?
Sketch the bullet's position versus time plots for the vertical and horizontal components. below the aim point.
What was the bullet's flight time?
Sketch the bullet's position versus time plots for the vertical and horizontal components.
|
| 3. |
25 pts. |
A rocket is fired vertically from rest and ascends with a constant acceleration
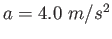 for a time for a time 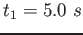 .
It's fuel is then exhausted and it continues as a free-fall particle.
Starting from the equations for the vertical position and velocity of the rocket,
what is the maximum altitude .
It's fuel is then exhausted and it continues as a free-fall particle.
Starting from the equations for the vertical position and velocity of the rocket,
what is the maximum altitude  and the total time and the total time 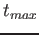 elapsed from takeoff until the rocket reaches its highest point?
elapsed from takeoff until the rocket reaches its highest point?
|
Physics 131-01 Equations
Physics 131-01 Constants
Speed of Light (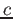 ) ) |
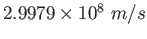 |
proton/neutron mass |
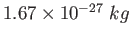 |
 |
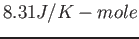 |
 |
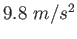 |
| Gravitation constant |
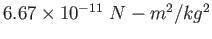 |
Earth's radius |
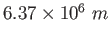 |
| Earth-Moon distance |
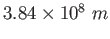 |
Electron mass |
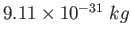 |