Physics 131-04 Test 3

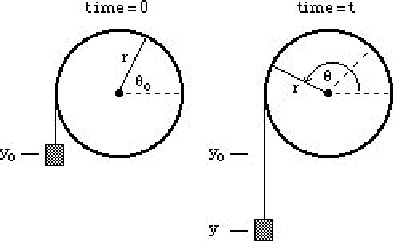
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.

Signature height0pt depth1pt width3in

Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

1. Suppose the mass of object 1 is greater than that of object 2 and that the objects are moving toward each other at the same speed so that
   
   $$m_{1}>m_{2}\quad \mbox{and}\quad {{\bf v}_{1}}=-{{\bf v}_{2}}$$
   
   

   
   
   

   
   

   $\parbox{3.25in}{Predict the relative magnitudes of the forces betwee... ...n each other. \par \rule{0.3in}{0.1pt} Object 2 exerts more force on object 1.}$

   
   
   
   
   
   
   
   

2. Why might an introductory physics student here on earth have the impression when throwing a ball against the floor or a wall that momentum isn't conserved?

   
   
   
   
   
   

3. Recall the lab where you studied a rotation collision by dropping a weight on a rotating disk. After dropping the weight on the rotating disk, the system will have a new moment of inertia. Derive a formula for the moment of inertia of a cylindrical-shaped weight of mass and radius revolving about the origin at a distance . (You will have to use the parallel axis theorem to do this.)

   
   
   
   
   
   

4. Consider the falling mass in the figure below. Suppose you are standing on your head so that the positive y-axis is pointing down. Using the relationships between the linear and angular variables, derive the rotational kinematic equation for constant accelerations for $y$. Warning: Don't just write the analogous equations! Show the substitutions needed to derive the equations on the right from those on the left.

   
   

   

   
   
   

   
   
   

5. A long, flexible, heavy pole cam be very useful for a tightrope walker. Why?

   
   
   
   
   
   

6. Suppose you are standing on a turntable that can freely rotate. When you hold a rotating bicycle wheel in front of you with its axis vertical you are at rest. If you now rotate the bike wheel so its axis points down, what happens to you? Explain your reasoning.

   
   
   
   
   
   

height0pt depth1pt width5.0in

Do not write below this line.

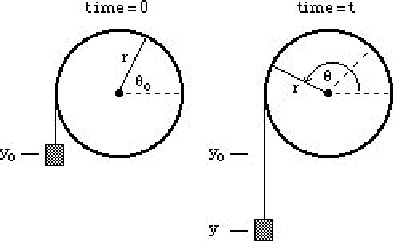
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1.	12 pts.	Three carts of mass $m_1 = 4~kg$, $m_2 = 10~kg$, and $m_3 = 3~kg$ move on a frictionless, horizontal track with speeds $v_1 = 3~m/s$, $v_2 = 2~m/s$, and $v_3=-5~m/s$ as shown in the figure. Velcro couplers make the carts stick together after colliding. What is the velocity of the train of three carts?
2.	20 pts.	A space station shaped like a wheel has a radius $r_s = 200~m$ and a moment of inertia $I_s = 2\times 10^9~kg-m^2$. A crew of 100 is living on the rim and the stations rotation causes the crew to experience an apparent free-fall acceleration of $g$. When 50 people move to the center of the station the angular speed changes. Assume the average mass of each inhabitant is $m=60~kg$. What apparent free-fall acceleration is experienced by the managers remaining in the rim?

3.

20 pts.

A construction worker was injured when a wooden beam that was partially supporting a porch broke off, swung down, and hit the worker in the head just as the person was walking by. You are an expert witness in the court case. The initial configuration of the beam is shown in the figure below with a length $l_h$, mass $m_h$, and an initial angle $\theta_h$. It is attached to a pivot at the bottom. The top of the worker's head is the same height as the pivot. Treat the beam as a uniform rod and neglect friction. What is the angular speed of the beam as it strikes the worker in the head in terms of $l_h$, mass $m_h$, and $\theta_h$ and any other constants?

height0pt depth1pt width5.0in

Do not write below this line.

Physics 131-4 Exam Sheet, Test 3

$$\Delta \vec r = \vec r_{finish} - \vec r_{start} \quad \Delta \vec v = \vec v_{finish} - \vec v_{start}$$

$$\langle \vec v \rangle = {\Delta \vec r \over \Delta t} \qqu... ...ta t \to 0} {\vec r (t+\Delta t) - \vec r(t) \over \Delta t}$$

$$\langle \vec a \rangle = {\Delta \vec v \over \Delta t} \qqu... ...lta t \to 0} {\vec v(t+\Delta t) - \vec v(t) \over \Delta t}$$

$$x(t) = {1 \over 2}at^2 + v_0t + y_0 \quad v = at + v_0 \quad... ...er r} \quad ( \vec v \perp \vec r \quad \vec v \perp \vec a_c)$$

$$\vec F_{net} = \sum_i \vec F_i = m \vec a = {d \vec p \over dt} \qquad \vec F_{AB} = -\vec F_{BA}$$

$$\vert\vec F_f\vert = \mu N \quad \vert\vec F_c\vert = m {v^2... ...} \quad \vec F_s(x) = -kx\hat i \quad \vec F_g(y) = -mg\hat j$$

$$W = \int \vec F \cdot d\vec s = \int \vert\vec F\vert ~\ve... ...a = \Delta KE = -\Delta U \quad KE = {1 \over 2} mv^2 \quad$$

$$KE_0 + U_0 = KE_1 + U_1 \quad KE = KE_{cm} + KE_{rot} \quad KE_{rot} = {1 \over 2} I \omega^2 \quad$$

$$U_s(x) = {1 \over 2} kx^2 \quad U_g(y) = mgy \quad U_G = \fr... ..._2}{r} \quad \vec p = m \vec v \quad \vec p_0 = \vec p_1 \quad$$

$$\theta = {s \over r} \quad \omega = {v_T \over r} = {d\theta... ... + Mh^2 \quad \vec r_{cm} = \frac{\sum m_i \vec r_i}{\sum m_i}$$

$$\vert\vec \tau \vert = r F\sin\phi = I\alpha = \left \vert\f... ...mv\sin \phi = I \omega \quad L_0 = L_1 \quad v_{cm} = r\omega$$

$$\vec A = A_x \hat i + A_y \hat j + A_z \hat k \qquad {dA \ov... ... 0 \qquad {dt \over dt} = 1 \qquad {dt^2 \over dt} = 2t \qquad$$

$$\int f(x)dx = \lim_{\Delta x \rightarrow 0} \sum f(x_i) \D... ... x \qquad \int dx = x + c \qquad \int x dx = {x^2 \over 2} + c$$

$$\sin \theta = {opp \over hyp} \quad \cos \theta = {adj \over... ...over adj} \quad x^2 + y^2 + z^2 = R^2 \quad \rho = {m \over V}$$

$$x = {-b \pm \sqrt{b^2 -4ac} \over 2a} \quad C = 2 \pi r \qua... ...pi r^2 \quad Area = {1 \over 2}bh \quad Area = 4 \pi r^2 \quad$$

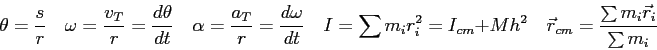
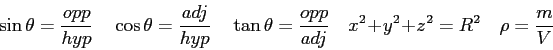
Speed of Light ($c$)	$2.9979\times 10^8~m/s$	proton/neutron mass	$1.67\times 10^{-27}~kg$
$R$	$8.31J/K-mole$	$g$	$9.8~m/s^2$
Gravitation constant	$6.67 \times 10^{-11}~N-m^2/kg^2$	Earth's radius	$6.37\times 10^6~m$
Earth-Moon distance	$3.84\times 10^8~m$	Electron mass	$9.11\times 10^{-31}~kg$