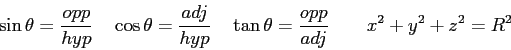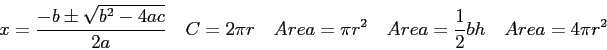Physics 131-04 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
- A cart is moving toward the right and slowing down, as shown in the diagrams
below. Draw arrows above the cart representing the magnitudes and directions
of the net (combined) forces you think are needed on the cart at
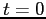 s,
s,
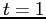 s, etc. to maintain its motion with a steadily decreasing velocity.
Assume that friction is so small that it can be ignored. Explain the reasons for your answers.
s, etc. to maintain its motion with a steadily decreasing velocity.
Assume that friction is so small that it can be ignored. Explain the reasons for your answers.

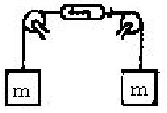
- Suppose you were to hang equal masses of
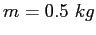 in the configuration shown below with the spring scale. Predict the tension in the string and the reading on the
spring scale.
Explain your reasoning.
in the configuration shown below with the spring scale. Predict the tension in the string and the reading on the
spring scale.
Explain your reasoning.
- Is the gravitational acceleration ``constant'',
 , really a constant? Explain.
, really a constant? Explain.
- Consider a ball dropped from rest near the Earth's surface with
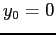 and positive is down.
Using the definition of work, show that
and positive is down.
Using the definition of work, show that 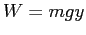 when an object is dropped
through a distance
when an object is dropped
through a distance  . Clearly show your reasoning.
. Clearly show your reasoning.
- The velocity
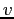 of the falling object in the previous question is related to the position
of the falling object in the previous question is related to the position  by
by
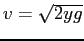 .
Combine this equation with the result in question 4 to show in theory
the work done on a mass falling under the influence of the gravitational attraction
exerted on it by the earth is given by the work-kinetic-energy theorem. Clearly show your reasoning.
.
Combine this equation with the result in question 4 to show in theory
the work done on a mass falling under the influence of the gravitational attraction
exerted on it by the earth is given by the work-kinetic-energy theorem. Clearly show your reasoning.
- Consider the figure below showing the potential energy
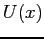 of a one-dimensional system as a function of position.
What is the maximum value of the mechanical energy
of a one-dimensional system as a function of position.
What is the maximum value of the mechanical energy 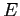 if the particle is to be trapped in
the potential well, i.e., the region
if the particle is to be trapped in
the potential well, i.e., the region 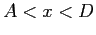 ? Explain your reasoning.
? Explain your reasoning.
![\includegraphics[width=2.5in]{f2.ps}](img56.png)
height0pt depth1pt width5.0in
Do not write below this line.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
12 pts. |
How fast can you set the Earth moving?
In particular, when you jump straight up as high as you can, what is the maximum recoil speed that you give to the Earth?
Assume you have a mass 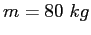 and can raise your center of gravity by a distance and can raise your center of gravity by a distance 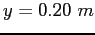 .
Your initial speed .
Your initial speed 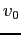 is related to the final height by is related to the final height by
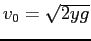 . .
|
| 2. |
15 pts. |
The figure below shows what is known as a conical pendulum.
The mass 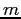 , attached to a string, moves in a horizontal circle of radius , attached to a string, moves in a horizontal circle of radius 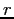 , with tangential velocity , with tangential velocity 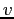 .
What is the angle that the string makes with the axis of the cone that the pendulum sweeps out
in terms of .
What is the angle that the string makes with the axis of the cone that the pendulum sweeps out
in terms of 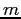 , , 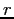 , , 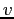 , and any additional constants? , and any additional constants?
|
| 3. |
25 pts. |
A new event has been proposed for the Winter Olympics.
An athlete will sprint a distance 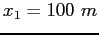 , starting from rest,
and leap into a bobsled of mass , starting from rest,
and leap into a bobsled of mass 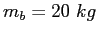 .
The person and the bobsled will slide down a ice-covered ramp of length .
The person and the bobsled will slide down a ice-covered ramp of length 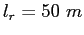 and tilted at an angle
and tilted at an angle
 to the horizontal.
At the bottom of the slope awaits a spring with spring constant to the horizontal.
At the bottom of the slope awaits a spring with spring constant 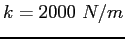 .
The athlete who compresses the spring the most wins.
The US entry in the competition Lisa has a mass .
The athlete who compresses the spring the most wins.
The US entry in the competition Lisa has a mass 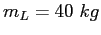 and she can reach a maximum velocity
and she can reach a maximum velocity 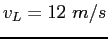 in the 100-m dash.
How far will Lisa compress the spring?
Ignore any friction with the ice. in the 100-m dash.
How far will Lisa compress the spring?
Ignore any friction with the ice.
![\includegraphics[width=3.0in]{prob3b.eps}](img27.png)
|
Physics 131-1 Exam Sheet, Test 2
Speed of Light ( ) ) |
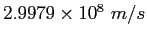 |
proton/neutron mass |
 |
 |
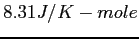 |
 |
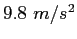 |
| Gravitation constant |
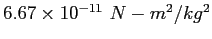 |
Earth's radius |
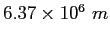 |
| Earth-Moon distance |
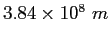 |
Earth mass |
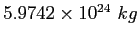 |
| Electron mass |
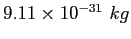 |
Moon mass |
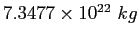 |


![\includegraphics[width=2.5in]{f2.ps}](img56.png)


![\includegraphics[width=2.5in]{f2.ps}](img56.png)
![\includegraphics[width=2.0in]{ucm2.ps}](img19.png)