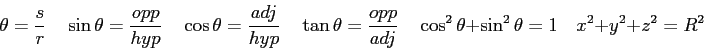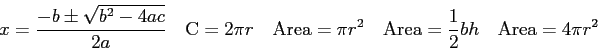
![\includegraphics[height=1.5in]{question5.eps}](img36.png)
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (9 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.



![\includegraphics[height=1.5in]{question5.eps}](img36.png)
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 15 pts. | The astronaut orbiting the Earth in the figure is docking with the Westar VI satellite.
The satellite is in an orbit 650 km above the Earth's surface where the free-fall acceleration
is
|
| 2. | 20 pts. | An astronaut on a strange planet finds she can jump a maximum horizontal distance
|
| 3. | 20 pts. | Some cars now carry `black boxes' like those on airplanes that collect data on speed, brake status,
and other information when the air bags are activated.
Suppose you are a lawyer and your client was in a car accident.
Your client claims he was driving at the speed limit of |
| Speed of Light ( |
|
proton/neutron mass |
|
| Gravitation constant |
|
Earth's radius |
|
| Earth-Moon distance |
|
Electron mass |
|