Physics 131-04 Final Exam
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Consider the following scenario from the Twins Paradox of Special Relativity.
As a space-faring twin's craft
recedes from the Earth it is moving at a constant speed. Since no
inertial frame can be considered ``better'' than any other there
is nothing physically inconsistent with the view that the space-faring
twin is observing the Earth recede from her at a constant velocity.
Hence, the space-faring twin will observe clocks on the Earth to move
slowly and the Earth-bound twin will age at a slower rate than the
space-faring one. Is this reasoning flawed? Explain.
- A spacecraft has the shape of a sphere when viewed from an inertial frame at rest with respect to the
spacecraft.
If it moves past an observer on Earth with a speed of
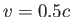 ,
what shape does the observer measure for the spacecraft? Explain.
,
what shape does the observer measure for the spacecraft? Explain.
- In the bottom panel of the figure below sketch the acceleration versus time graph that would match
the velocity versus time plot that is shown in the top panel of the figure. State the reasoning behind your sketch.
![\includegraphics[height=1.75in]{f1.eps}](img70.png)
- Recall the lab where you placed a motion sensor at the bottom of a dynamics track inclined upward
and you gave a dynamics cart a gentle push away from the motion detector.
For each part of the motion - away from the detector, at the turning point,
and toward the detector, predict in the table below whether the velocity
will be positive, zero or negative. Also indicate whether the acceleration is
positive, zero or negative. Explain your reasoning.
| |
Moving Away |
Turning Around |
Moving Toward |
| Velocity |
|
|
|
| Acceleration |
|
|
|
- Consider the histogram shown below for two sets of possible fall times from different classes.
The average and standard deviation of the data is
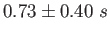 . How many peaks are in this
histogram? Do the average and standard deviation capture the full description of the data?
Why or why not.
. How many peaks are in this
histogram? Do the average and standard deviation capture the full description of the data?
Why or why not.
- For the configuration shown below, predict the reading in newtons on
the spring scale (
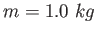 ). Explain your reasoning.
). Explain your reasoning.
- You have a spring scale hooked to a block on a flat, lab table.
Hold the spring scale at a 30
 angle with respect to the horizontal and use it to pull the block
a distance of 0.5 meters along the table surface so the
block moves at a constant speed.
Is this force larger or smaller
than if you pulled the block horizontally? Explain.
angle with respect to the horizontal and use it to pull the block
a distance of 0.5 meters along the table surface so the
block moves at a constant speed.
Is this force larger or smaller
than if you pulled the block horizontally? Explain.
- The figure below shows for graphs of position versus time for two bodies and their center of mass.
The two bodies undergo a completely inelastic, one-dimensional collision while moving along the
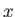 axis.
Which graphs correspond to physically impossible situations.
Explain your reasoning.
axis.
Which graphs correspond to physically impossible situations.
Explain your reasoning.
- The figures below show identical meter sticks, half wood and half steel, that are pivoted at the point
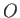 in figure (a) and at the point
in figure (a) and at the point  in figure (b).
The same force
in figure (b).
The same force 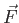 is applied at the points
is applied at the points 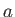 and
and 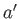 in figures (a) and (b) respectively.
The steel portion of the meter stick is heavier than the wood part.
Is the angular acceleration in the figure (b) the same, less than, or greater than the angular
acceleration in figure (a)?
Explain.
in figures (a) and (b) respectively.
The steel portion of the meter stick is heavier than the wood part.
Is the angular acceleration in the figure (b) the same, less than, or greater than the angular
acceleration in figure (a)?
Explain.
- A skater slides down three slopes of frictionless ice whose vertical heights
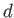 are identical.
Rank the slopes according to change in her kinetic energy produced along the slope, greatest first.
Explain your reasoning.
are identical.
Rank the slopes according to change in her kinetic energy produced along the slope, greatest first.
Explain your reasoning.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet for your work.
| 1. |
8 pts. |
An interstellar space probe is launched from the Earth.
After a brief period of acceleration it moves with a constant velocity 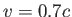 where
where  is the speed of light.
Its nuclear-powered batteries supply the energy to keep its data transmitter active continuously.
The batteries have a lifetime is the speed of light.
Its nuclear-powered batteries supply the energy to keep its data transmitter active continuously.
The batteries have a lifetime
 as measured in a rest frame.
How long do the batteries last as measured by Mission Control on Earth?
How far is the probe from the Earth when its batteries fail as measured by Mission Control? as measured in a rest frame.
How long do the batteries last as measured by Mission Control on Earth?
How far is the probe from the Earth when its batteries fail as measured by Mission Control?
|
| 2. |
8 pts. |
A man is reported to have fallen a distance 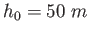 from a building,
landing on a metal ventilator box that he crushed to a depth from a building,
landing on a metal ventilator box that he crushed to a depth 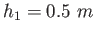 .
He suffered only minor injuries.
Ignoring air friction and treating his acceleration after hitting box as constant, how long
did it take for him to crush the box after he landed on it?
Assume he fell from rest. .
He suffered only minor injuries.
Ignoring air friction and treating his acceleration after hitting box as constant, how long
did it take for him to crush the box after he landed on it?
Assume he fell from rest.
|
| 3. |
8 pts. |
An object of mass 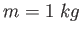 is observed to accelerate at is observed to accelerate at 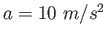 in a direction
in a direction
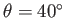 north of east as shown in the figure.
The force north of east as shown in the figure.
The force 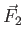 acting on the object has a magnitude acting on the object has a magnitude
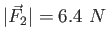 and is
directed north.
What is the magnitude and direction of the force and is
directed north.
What is the magnitude and direction of the force  ? ?
|
Continue 
Problems (continued). Clearly show all work for full credit.
| 4. |
8 pts. |
It takes  of work to stretch a Hooke's-Law spring a distance of work to stretch a Hooke's-Law spring a distance 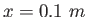 from its unstressed length.
What is the extra work
from its unstressed length.
What is the extra work 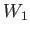 required to stretch it an additional required to stretch it an additional 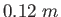 ? ?
|
| 5. |
8 pts. |
To measure the speed of a bullet, the following situation is set up.
A wooden block (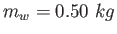 ) is put on top of a fencepost with a height of ) is put on top of a fencepost with a height of 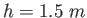 .
The bullet ( .
The bullet (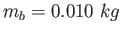 )
strikes the block from a perfectly horizontal direction and remains embedded in it.
The block is measured to fall )
strikes the block from a perfectly horizontal direction and remains embedded in it.
The block is measured to fall 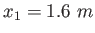 from the base of the post.
How fast was the bullet going? from the base of the post.
How fast was the bullet going?
|
| 6. |
10 pts. |
One of the components of an old grandfather clock consists of a uniform ring attached to a pivot
by a short, uniform rod.
It starts from a nearly vertical position as shown in the figure and is then released from rest.
What is the speed of the lowest point on the hoop at the bottom of the hoop's trajectory?
The mass and radius of the hoop are 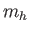 and and 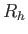 .
The length of the rod is .
The length of the rod is  and the mass is so small that we can ignore it.
Get your answer in terms of these quantities and any other necessary constants. and the mass is so small that we can ignore it.
Get your answer in terms of these quantities and any other necessary constants.
|
Physics 131-4 Final Exam Sheet
Speed of Light ( ) ) |
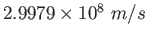 |
proton/neutron mass |
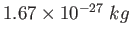 |
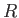 |
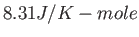 |
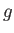 |
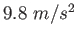 |
| Gravitation constant |
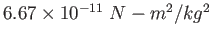 |
Earth's radius |
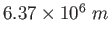 |
| Earth-Moon distance |
 |
Electron mass |
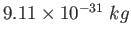 |
![\includegraphics[height=1.75in]{f1.eps}](img70.png)
![\includegraphics[height=1.75in]{f3.eps}](img5.png)
![\includegraphics[height=1.75in]{HR_F010_19.eps}](img8.png)
![\includegraphics[height=1.25in]{f6.eps}](img14.png)
![\includegraphics[height=2.0in]{f7.eps}](img16.png)
![\includegraphics[height=1.75in]{f1.eps}](img70.png)
![\includegraphics[height=1.75in]{f3.eps}](img5.png)
![\includegraphics[height=1.75in]{HR_F010_19.eps}](img8.png)
![\includegraphics[height=1.25in]{f6.eps}](img14.png)
![\includegraphics[height=2.0in]{f7.eps}](img16.png)
![\includegraphics[height=1.75in]{f9.eps}](img28.png)
![]()
![\includegraphics[height=2.0in]{Collision6.ps}](img38.png)
![\includegraphics[height=1.8in]{f10.eps}](img42.png)
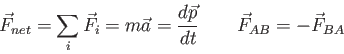
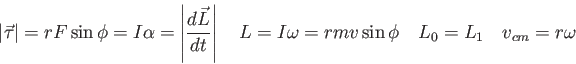
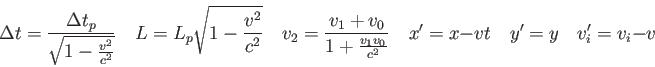
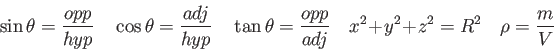
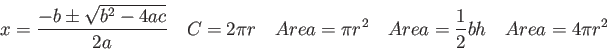
![\includegraphics[width=6.0in]{10t02a.ps}](img68.png)
![\includegraphics[width=6.0in]{10t02b.ps}](img69.png)