Physics 131-01 Final Exam
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (4 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- You are riding on a flat
surface in a cart at a velocity
 .
A stationary observer is nearby.
At
.
A stationary observer is nearby.
At  your coordinate systems coincide.
At
your coordinate systems coincide.
At  you fire the toy cannon at an angle of about
you fire the toy cannon at an angle of about  from the moving cart.
Consider a point
from the moving cart.
Consider a point
 on the
ball's trajectory in the stationary observer's reference frame. If
the moving observer's time frame is moving at the speed
on the
ball's trajectory in the stationary observer's reference frame. If
the moving observer's time frame is moving at the speed
 then what would the moving observer measure for
then what would the moving observer measure for  ? Call this horizontal
position of the moving observer
? Call this horizontal
position of the moving observer  .
.
- Consider the following scenario from the Twins Paradox of Special Relativity.
As a space-faring twin's craft
recedes from the Earth it is moving at a constant speed. Since no
inertial frame can be considered ``better'' than any other there
is nothing physically inconsistent with the view that the space-faring
twin is observing the Earth recede from her at a constant velocity.
Hence, the space-faring twin will observe clocks on the Earth to move
slowly and the Earth-bound twin will age at a slower rate than the
space-faring one. Is this reasoning flawed? Explain.
- How does the vertical acceleration of a projectile on the Earth influence the horizontal
acceleration? What is your evidence?
- In the figure below, what is the equation to estimate the average slope of the curve
at the highlighted point in terms of
 ,
,  ,
,  ,
and
,
and  ? How would you find the ``exact'' value of the slope at the
point in the figure between
? How would you find the ``exact'' value of the slope at the
point in the figure between  and
and  ?
?
![\includegraphics[height=1.75in]{equations_fig2.eps}](img78.png)
- Consider the histogram shown below for a set of possible fall times for an experiment
studying the acceleration of gravity.
What advantages does a histogram of these data have over calculating the average and standard deviation?
![\includegraphics[height=1.75in]{stats1.eps}](img79.png)
- You are sleeping at home over winter break and wake up to find the house
is on fire and smoke is pouring into the partially open bedroom door. The room
is so messy that you cannot get to the door. The only way to close the door
is to throw either a blob of clay or a super ball at the door --
there's not enough time to throw both.
Assuming that the clay blob and the super ball have the same mass, which would
you throw to close the door: the clay blob (which will stick to the door) or
the super ball (which will bounce back with almost the same velocity it had
before it collided with the door)? Give reasons for your choice, using any notions
you already have or any new concepts developed in physics such as force, momentum,
Newton's laws, etc. Remember, your life depends on it!
- An object can move along a horizontal line
(the + position axis). Assume that friction is so small that it can be ignored.
The object's velocity-time graph is shown below.
Draw the the shape of the acceleration-time and force-time graphs on the axes
below.
Explain your reasoning.
- Suppose that the force applied to the object in Question 7 were twice as large. Sketch
with dashed lines on the same axes above the force, acceleration, and velocity. Explain your
reasoning.
- The figure below shows three apples that are launched from the same level with the same speed.
One moves straight upward, one is launched at a small angle to the vertical, and one is launched
along a
frictionless incline.
Rank the apples according to their speed when they reach the level of the dashed line, greatest
first.
Explain.
![\includegraphics[height=1.5in]{apples.ps}](img80.png)
- In some motorcycle races, the riders drive over small hills and become airborne for short
periods of
time.
If the motorcycle racer keeps the throttle open while leaving the hill and going into the air,
the motorcycle
tends to nose upward.
Why?
Problems. Clearly show all reasoning for full credit.
Use a separate sheet for your work.
Continue 
Problems (continued). Clearly show all work for full credit.
Continue 
Problems (continued). Clearly show all work for full credit.
| 6. |
10 pts. |
The stars on the rim of our Milky Way Galaxy take about
750 million years (i.e.
 )
to orbit the
galactic core which is a distance )
to orbit the
galactic core which is a distance
 away.
They follow circular orbits.
What is the acceleration of these rim stars?
What galactic mass is required?
Assume, as usual, the mass of the galaxy
can be treated as a point at the center of the galaxy.
How does this compare to the galactic mass of away.
They follow circular orbits.
What is the acceleration of these rim stars?
What galactic mass is required?
Assume, as usual, the mass of the galaxy
can be treated as a point at the center of the galaxy.
How does this compare to the galactic mass of
 determined by counting the number of stars?
determined by counting the number of stars?
|
Table of Constants
Speed of Light ( ) ) |
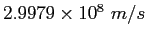 |
proton/neutron mass |
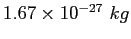 |
 |
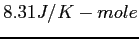 |
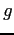 |
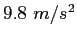 |
| Gravitation constant |
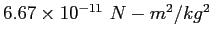 |
Electron mass |
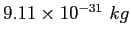 |
| Earth's mass |
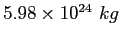 |
Earth's radius |
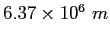 |
| Earth-Moon distance |
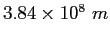 |
Earth-Sun distance |
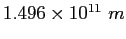 |
| Solar mass |
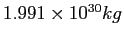 |
Solar radius |
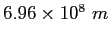 |
Table of Equations
![\includegraphics[height=1.75in]{equations_fig2.eps}](img78.png)
![\includegraphics[height=1.75in]{stats1.eps}](img79.png)


![\includegraphics[height=1.5in]{apples.ps}](img80.png)
![\includegraphics[height=1.75in]{equations_fig2.eps}](img78.png)
![\includegraphics[height=1.75in]{stats1.eps}](img79.png)


![\includegraphics[height=1.5in]{apples.ps}](img80.png)
![]()
![\includegraphics[height=3.0in]{10prob48.ps}](img36.png)
![]()
![\includegraphics[height=3.0in]{MilkyWayGalaxySun05.ps}](img44.png)






![\includegraphics[width=5.0in]{10t02a.ps}](img76.png)
![\includegraphics[width=5.0in]{10t02b.ps}](img77.png)