Physics 131-04 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (9 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
- What is the impulse-momentum theorem? Is it correct? What is your evidence?
- Suppose the mass of object 1 is much less than that of object 2 and that
it is pushing object 2 that has a dead motor so that both objects move in the
same direction at speed v.
Predict the relative magnitudes of the forces between object 1 and object 2.
Place a check next to your prediction.
Object 1 exerts more force on object 2.
The objects exert the same force on each other.
Object 2 exerts more force on object 1.
Explain the reasons for your answers.
- Suppose a particle is moving around in a circle with an angular velocity
that has a magnitude of
 associated with it. According to observer
#1, does the particle appear to be moving clockwise or counter clockwise? How
about the direction of the particle's motion according to observer #2?
Is the clockwise vs. counterclockwise designation a good way to determine
the direction associated with
associated with it. According to observer
#1, does the particle appear to be moving clockwise or counter clockwise? How
about the direction of the particle's motion according to observer #2?
Is the clockwise vs. counterclockwise designation a good way to determine
the direction associated with 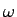 in an unambiguous way? Why or why not?
in an unambiguous way? Why or why not?
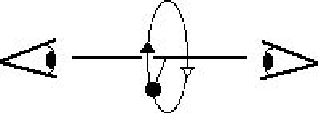 (-190,-12)Observer 1 Observer 2
(-190,-12)Observer 1 Observer 2
- The plot below shows the
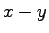 position of a ball bearing after it was hit by another, rolling ball bearing.
The time and positions of the struck bearing are shown in the table.
How would you determine the speed of the bearing? Show any equations your would use.
position of a ball bearing after it was hit by another, rolling ball bearing.
The time and positions of the struck bearing are shown in the table.
How would you determine the speed of the bearing? Show any equations your would use.
![\includegraphics[height=1.25in]{f1.eps}](img54.png)
|
time(s) |
x (cm) |
y (cm) |
|
time(s) |
x (cm) |
y (cm) |
|
2.5012 |
22.72 |
21.568 |
|
2.9068 |
11.52 |
17.28 |
|
2.5688 |
22.72 |
21.568 |
|
2.9744 |
9.004 |
16.44 |
|
2.6364 |
22.41 |
21.464 |
|
3.042 |
6.596 |
15.71 |
|
2.704 |
18.85 |
20.31 |
|
3.1096 |
4.4 |
15.45 |
|
2.7716 |
16.54 |
19.26 |
|
3.1772 |
1.88 |
13.61 |
|
2.8392 |
14.13 |
18.11 |
|
|
|
|
- The figure below shows four gears that rotate together because of the friction between them so they turn without slipping.
Gears 1 and 4 have radius
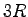 , gear 2 has radius
, gear 2 has radius 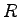 , and gear 3 has radius
, and gear 3 has radius 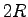 .
Gear 2 is forced to rotate by a motor.
Rank the four gears according to the angular speed of the gears with the greatest first.
Explain your reasoning.
.
Gear 2 is forced to rotate by a motor.
Rank the four gears according to the angular speed of the gears with the greatest first.
Explain your reasoning.
![\includegraphics[height=0.7in]{gears.eps}](img55.png)
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
Equations and Constants
Speed of Light (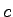 ) ) |
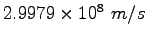 |
proton/neutron mass |
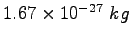 |
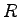 |
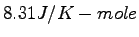 |
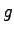 |
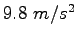 |
| Gravitation constant |
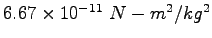 |
Earth's radius |
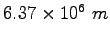 |
| Earth-Moon distance |
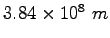 |
Electron mass |
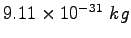 |

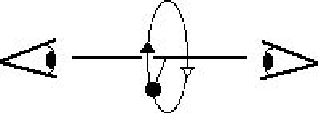 (-190,-12)Observer 1 Observer 2
(-190,-12)Observer 1 Observer 2
![\includegraphics[height=1.25in]{f1.eps}](img54.png)
![\includegraphics[height=0.7in]{gears.eps}](img55.png)
![\includegraphics[height=1.5in]{bounce.eps}](img25.png)
![\includegraphics[height=1.5in]{twirling4.eps}](img26.png)

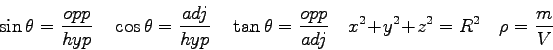
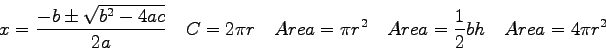
![\includegraphics[width=6.0in]{10t02a.ps}](img51.png)
![\includegraphics[width=6.0in]{10t02b.ps}](img52.png)