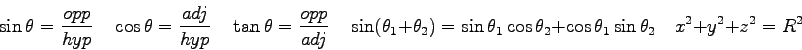Physics 131-04 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
- Newton's Second Law states that
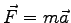 . Why should you believe this? What is your evidence?
. Why should you believe this? What is your evidence?
- A cart is moving toward the right and slowing down, as shown in the diagrams
below. Draw arrows above the cart representing the magnitudes and directions
of the net (combined) forces you think are needed on the cart at
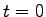 s,
s,
 s, etc. to maintain its motion with a steadily decreasing velocity.
s, etc. to maintain its motion with a steadily decreasing velocity.
Explain the reasons for your answers.
- Take a look at the diagram below. Can the strongest member of your group stretch
a string or rope so that it is perfectly horizontal when a 10 kg mass is hanging
from it? In other words, can the string provide a force that just balances the
force exerted by the mass? Explain.
![\includegraphics[width=2.5in]{newton_fig7.eps}](img54.png)
- Recall the lab where we used toy airplanes to study centripetal force.
In that lab we used video analysis to measure
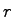 , the radius of the airplane's circular path, and a ruler to measure
, the radius of the airplane's circular path, and a ruler to measure
 , the
total length of the string that is actually rotating below the pivot point.
Using these two distances (
, the
total length of the string that is actually rotating below the pivot point.
Using these two distances (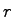 and
and  ),
calculate the angle the string makes with
the horizontal. Clearly show your reasoning.
),
calculate the angle the string makes with
the horizontal. Clearly show your reasoning.
- Consider the result below for a measurement of the kinetic, potential, and total energy of
a falling ball. Does the mechanical energy appear
to be conserved within experimental uncertainties? How would you quantitatively estimate
the value of the experimental uncertainty? Once you establish the method apply it to your data.
The average value of the total energy in the figure is
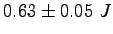 .
.
![\includegraphics[height=1.75in]{f1.eps}](img55.png)
- The figure below shows four situations - one in which an initially stationary block is dropped from
rest (part (1) on the left-hand side of the figure below) and three in which the block is allowed to slide down frictionless ramps (parts (2)-(4)
in the figure).
Rank the situations according to the speed of the block at point
 with the greatest first.
Explain your reasoning.
with the greatest first.
Explain your reasoning.
![\includegraphics[width=3.0in]{KEquestion.ps}](img56.png)
height0pt depth1pt width5.0in
Do not write below this line.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
15 pts. |
An object with mass  is placed on a frictionless, horizontal table
and connected to a cable that passes over a pulley and then is fastened to another object
with is placed on a frictionless, horizontal table
and connected to a cable that passes over a pulley and then is fastened to another object
with  as shown below.
What is the acceleration of each object and what is the tension in the string? as shown below.
What is the acceleration of each object and what is the tension in the string?
![\includegraphics[width=2.5in]{table.eps}](img27.png)
|
| 2. |
17 pts. |
A block of mass 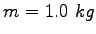 is pushed against a horizontal spring of negligible mass until the spring
is compressed a distance is pushed against a horizontal spring of negligible mass until the spring
is compressed a distance  . See the figure below.
The force constant of the spring is . See the figure below.
The force constant of the spring is 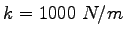 .
When .
When
l3.0in
![\includegraphics[width=3.1in]{energy2.ps}](img14.png)
the spring is released the block travels along a frictionless, horizontal surface to point 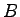 , the bottom
of a vertical circular track of radius , the bottom
of a vertical circular track of radius 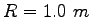 , and continues to move up the track.
The speed of the block at the bottom of the track is , and continues to move up the track.
The speed of the block at the bottom of the track is  and the block experiences an average
friction force and the block experiences an average
friction force 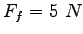 while sliding up the track.
What is while sliding up the track.
What is  ?
What is the speed ?
What is the speed 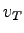 of the block at the top of the track?
Assume it has enough speed to make it to the top. of the block at the top of the track?
Assume it has enough speed to make it to the top.
|
| 3. |
20 pts. |
The space shuttle is in a high, circular orbit a distance 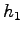 above the surface of the Earth.
The crew performs an experiment that needs to take place far away from the spacecraft so
a payload of mass above the surface of the Earth.
The crew performs an experiment that needs to take place far away from the spacecraft so
a payload of mass  is `lowered' toward the Earth on a massless rope of length is `lowered' toward the Earth on a massless rope of length  .
The shuttle and the payload are flying along in equilibrium so the spacecraft, the payload, and the rope are all aligned
along a radius from the center of the Earth to the shuttle.
The period of the shuttle's orbit .
The shuttle and the payload are flying along in equilibrium so the spacecraft, the payload, and the rope are all aligned
along a radius from the center of the Earth to the shuttle.
The period of the shuttle's orbit 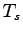 is known, the mass is known, the mass  of the payload is much smaller than the shuttle mass and of the payload is much smaller than the shuttle mass and
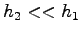 .
How is the shuttle's period .
How is the shuttle's period 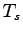 related to the payload's period related to the payload's period 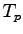 ?
What is the tension ?
What is the tension 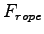 in the rope in terms of in the rope in terms of 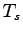 , , 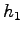 , ,  , ,  and any other known constants?
Be careful with the notation because
we sometimes use and any other known constants?
Be careful with the notation because
we sometimes use 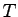 to refer to tension and the period of the orbit. to refer to tension and the period of the orbit.
|
Physics 131-4 Exam Sheet, Test 2
Speed of Light (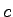 ) ) |
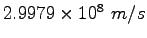 |
proton/neutron mass |
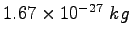 |
 |
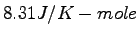 |
 |
 |
| Gravitation constant |
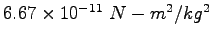 |
Earth's radius |
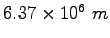 |
| Earth-Moon distance |
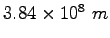 |
Earth mass |
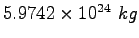 |
| Electron mass |
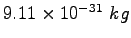 |
Moon mass |
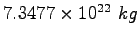 |

![\includegraphics[width=2.5in]{newton_fig7.eps}](img54.png)
![\includegraphics[height=1.75in]{f1.eps}](img55.png)
![\includegraphics[width=3.0in]{KEquestion.ps}](img56.png)

![\includegraphics[width=2.5in]{newton_fig7.eps}](img54.png)
![\includegraphics[height=1.75in]{f1.eps}](img55.png)
![\includegraphics[width=3.0in]{KEquestion.ps}](img56.png)
![\includegraphics[width=3.1in]{energy2.ps}](img14.png)