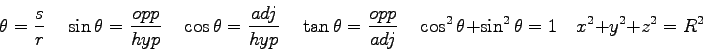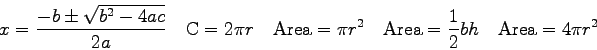Physics 131-04 Test 1


I pledge that I have neither given nor received unauthorized assistance during the completion of this work.


Signature height0pt depth1pt width3in


Questions (9 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

  1. Draw the velocity graphs for an object whose motion produced the position-time graphs shown below on the left. Position is in meters and velocity in meters per second. Note: Unlike most real objects, you can assume these objects can change velocity so quickly that it looks instantaneous with this time scale. Explain your reasoning.



    \includegraphics{relating_fig5.eps}



  2. Describe how you must move to produce a position vs. time graph with the shape shown.

    \includegraphics{position1.eps}

  3. What are the general rules to predict the sign and direction of the acceleration if you know the sign of the velocity (i.e., the direction of motion) and whether the object is speeding up or slowing down?

  4. Refer to the diagram below. Explain why, at the two points shown on the circle, the angle between the position vectors at times \( t_{1} \) and \( t_{2} \) is the same as the angle between the velocity vectors at times \( t_{1} \) and \( t_{2} \).

    \includegraphics{circ_motion_fig3.eps}

  5. The figure below shows the paths of two thrown balls. Ignoring the effects of air resistance, rank the two paths according to (a) time of flight, (b) initial vertical velocity component, (c) initial horizontal velocity component, and (d) initial speed. Place the greatest first in each part.

    \includegraphics[height=1.5in]{balls.eps}

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1. 15 pts. The astronaut orbiting the Earth in the figure is docking with the Westar VI satellite. The satellite is in an orbit 650 km above the Earth's surface where the free-fall acceleration is $a = 8.09 ~m/s^2$. The radius of the Earth is in the table below. What is the time interval for one complete orbit?


\includegraphics[height=1.25in]{westar6.ps}

2. 20 pts. A driver moving at $v_0 = 35~m/s$ enters a one-lane tunnel. The driver sees a slow-moving van a distance $x_1= 50~m$ ahead going $v_1=15~m/s$ and slams on the breaks. The road is wet so the acceleration of the breaks is only $a = -2~m/s^2$. How long after applying the breaks does the car hit the van?

3. 20 pts. During a volcanic eruption chunks of rock are blasted out of the volcano. These projectiles are called volcanic bombs. Consider the figure below of Mount Fuji in Japan. A volcanic bomb is launched at an angle $\theta = 35^\circ$ from point A in the figure and it eventually lands at point B. How long would the people at point B have to get out of the way once the the rock leaves the mouth of the volcano? The mouth of the volcano is a distance $y_0 = 3.3\times 10^3~m$ above the landing spot which is a distance $x_f = 9.4\times 10^3~m$ downrange from the mouth of the volcano.

\includegraphics[height=2.0in]{MountFuji.ps}


Physics 131-04 Constants

Speed of Light ($c$) $2.9979\times 10^8~m/s$ proton/neutron mass $1.67\times 10^{-27}~kg$
$R$ $8.31J/K-mole$ $g$ $9.8~m/s^2$
Gravitation constant $6.67 \times 10^{-11}~N-m^2/kg^2$ Earth's radius $6.37\times 10^6~m$
Earth-Moon distance $3.84\times 10^8~m$ Electron mass $9.11\times 10^{-31}~kg$

Physics 131-04 Equations



\begin{displaymath} \Delta x = x_{finish} - x_{start} \qquad \Delta \vec r = \ve... ...{start} \quad \Delta \vec v = \vec v_{finish} - \vec v_{start} \end{displaymath}


\begin{displaymath} \bar v = \langle v \rangle = {\Delta x \over \Delta t} \quad... ...\to 0} {x (t+\Delta t) - x(t) \over \Delta t} = {dx \over dt} \end{displaymath}


\begin{displaymath} \bar a = \langle a \rangle = {\Delta v \over \Delta t} \quad... ... \to 0} {v(t+\Delta t) - v(t) \over \Delta t} = {dv \over dt} \end{displaymath}


\begin{displaymath} x = {1 \over 2}at^2 + v_0t + x_0 \qquad v = at + v_0 \qquad a_g = -g \end{displaymath}


\begin{displaymath} \vec A = A_x \hat i + A_y \hat j + A_z \hat k \quad \vec A +... ... B = (A_x + B_x)\hat i + (A_y + B_y)\hat i + (A_z + B_z)\hat i \end{displaymath}


\begin{displaymath} a_c = {v^2 \over r} \qquad \vec v \perp \vec r \qquad \vec v \perp \vec a_c \end{displaymath}


\begin{displaymath} \vec v = {d \vec r \over dt} = {dx \over dt}\hat i + {dy \... ...over dt}\hat i + {dv_y \over dt}\hat j + {dv_z \over dt}\hat k \end{displaymath}


\begin{displaymath} \theta = {s \over r}\quad \sin \theta = {opp \over hyp} \qua... ...uad \cos^2\theta + \sin^2\theta =1 \quad x^2 + y^2 + z^2 = R^2 \end{displaymath}


\begin{displaymath} x = {-b \pm \sqrt{b^2 -4ac} \over 2a} \quad {\rm C} = 2 \pi ... ... {\rm Area} = {1 \over 2}bh \quad {\rm Area} = 4 \pi r^2 \quad \end{displaymath}


\begin{displaymath} {\rm Volume} = {4 \over 3} \pi r^3 \qquad {\rm Volume} = \pi r^2 l \qquad \end{displaymath}