Physics 131-4 Final Exam
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (4 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- You are riding on a flat
surface in a cart at a velocity
 .
You point a toy cannon straight up in the air, fire off
a shot, and record the vertical position as a function of time.
An observer on the ground also measures the vertical position as a function of time.
How do the two plots differ in appearance? Explain your answer.
.
You point a toy cannon straight up in the air, fire off
a shot, and record the vertical position as a function of time.
An observer on the ground also measures the vertical position as a function of time.
How do the two plots differ in appearance? Explain your answer.
- Consider the following scenario from the twins paradox. As the space-faring twin's craft
recedes from the Earth it is moving at a constant speed. Since no
inertial frame can be considered ``better'' than any other there
is nothing physically inconsistent with the view that the space-faring
twin is observing the Earth recede from her at a constant velocity.
Hence, the space-faring twin will observe clocks on the Earth to move
slowly and the Earth-bound twin will age at a slower rate than the
space-faring one. Is this reasoning flawed? Why or why not?
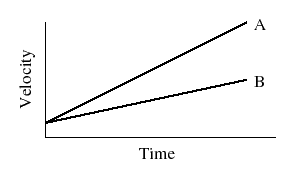
- The velocity graph below shows the motion of two objects, A and B. Answer
the following questions separately. Explain your answers. (1) What does
the intersection mean? (2) Can one tell which object is ``ahead''? Explain your reasoning.
(define ``ahead'')
- Consider the histogram shown below for two sets of possible fall times from different classes.
The average and standard deviation of the data is
 .
Do the average and standard deviation capture the full description of the data? Why or why not?
.
Do the average and standard deviation capture the full description of the data? Why or why not?
![\includegraphics[height=2.25in]{SampleHist1.eps}](img71.png)
- Use Newton's law of universal gravitation to show that the magnitude of the acceleration due
to gravity on an object of mass
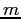 at a height
at a height  above the surface of the earth is given by the following expression.
above the surface of the earth is given by the following expression.
Hint: Because of the spherical symmetry of the Earth you can treat the mass
of the Earth as if it were all concentrated at a point at the Earth's center.
- Assume that an object is accelerating in a circle of constant radius,
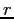 .
Using the relationship
.
Using the relationship 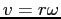 , take the derivative of
, take the derivative of  with
respect to time to find the tangential acceleration of the object.
Show that the linear acceleration,
with
respect to time to find the tangential acceleration of the object.
Show that the linear acceleration, 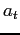 , tangent to the circle is related to the angular
acceleration,
, tangent to the circle is related to the angular
acceleration, 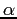 , by the equation
, by the equation
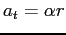 .
.
- Using the diagram below, draw a dotted line in the direction you think your
two cars will move after a collision between cars with equal masses and velocities.
Explain your reasoning in the space below.
![\includegraphics[height=1.75in]{twod_collision_crasha.eps}](img72.png)
- Suppose an object is lifted through a distance
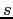 near the surface of the Earth and then allowed to fall.
Starting from the definition of work as
near the surface of the Earth and then allowed to fall.
Starting from the definition of work as
 show
show 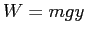 when the object is dropped through a distance
when the object is dropped through a distance 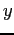 .
Explain your reasoning.
.
Explain your reasoning.
- Suppose somebody tosses you a raw egg and you catch it. In physics jargon, one
would say (in a very official tone of voice) that ``the egg and the
hand have undergone an inelastic collision.'' What is the relationship
between the force you have to exert on the egg to stop it, the time it takes
you to stop it, and the momentum change that the egg experiences? You ought
to have some intuition about this matter. In more ordinary language, would you
catch an egg slowly or fast?
- The figure below shows the velocity and acceleration of a particular instant in three
situations. In which situations is the speed not changing. Explain.
![\includegraphics[height=1.25in]{acceleration1.ps}](img73.png)
- The figure below shows an overhead view of two, identical stones traveling in circles over a frictionless
surface.
Each stone is tied to a cord whose opposite end is anchored at the center of the circle.
Is the tension in the longer cord greater than, less than, or the same as the tension in the shorter
cord if the stones travel with the same period of motion? Explain.
![\includegraphics[height=1.0in]{rocks.eps}](img74.png)
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
|
|
|
| 3. |
10 pts. |
Consider a conical pendulum with a bob of mass 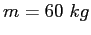 on a wire of length on a wire of length
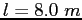 and making an angle and making an angle
 with the vertical (see the figure).
What are the horizontal and vertical components of the force exerted by the wire on the
pendulum and what is the radial acceleration of the bob? with the vertical (see the figure).
What are the horizontal and vertical components of the force exerted by the wire on the
pendulum and what is the radial acceleration of the bob?
![\includegraphics[height=1.7in]{pendulum1.ps}](img36.png)
|
| 4. |
10 pts. |
A freight car of mass  rolls along rails with negligible friction.
The car is brought to rest by a combination of two springs as illustrated in the figure.
Both springs obey Hooke's law with rolls along rails with negligible friction.
The car is brought to rest by a combination of two springs as illustrated in the figure.
Both springs obey Hooke's law with
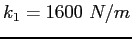 and and
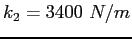 .
After the first spring compresses a distance .
After the first spring compresses a distance 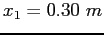 , the second spring acts with the first
to increase the force as additional compression as shown in the graph.
The freight car comes to a rest a distance , the second spring acts with the first
to increase the force as additional compression as shown in the graph.
The freight car comes to a rest a distance 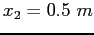 after first contacting the two-spring
system.
What is the freight car's initial speed? after first contacting the two-spring
system.
What is the freight car's initial speed?
![\includegraphics[height=1.5in]{freightCar5.ps}](img37.png) (5,-15) (5,-15)![\includegraphics[height=1.65in]{freightCar3.eps}](img31.png)
|
| 5. |
10 pts. |
A catapult launches a rocket at an angle
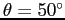 above the horizontal
with an initial speed above the horizontal
with an initial speed 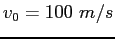 .
The rocket engine immediately starts a burn and for .
The rocket engine immediately starts a burn and for
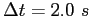 the rocket moves along its
initial line of motion with an acceleration the rocket moves along its
initial line of motion with an acceleration
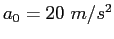 .
Then its engine fails and the rocket proceeds to move in free-fall.
What is the maximum altitude reached by the rocket? .
Then its engine fails and the rocket proceeds to move in free-fall.
What is the maximum altitude reached by the rocket?
|
| 6. |
10 pts. |
Global warming is a cause for concern because even small changes in the
Earth's temperature can have significant consequences.
For example, if the Earth's polar ice caps were to melt entirely, the resulting additional
water in the oceans would flood many coastal cities.
Would it appreciably change the length of a day?
Model each polar ice cap as a flat disk of mass
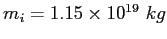 , radius , radius
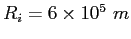 , and centered on the axis of rotation of the rest of the Earth.
Treat the rest of the Earth as a uniform sphere of mass and radius given in the table of constants.
An approximate representation of an Arctic polar cap of these dimensions is shown
as the unrealistically red disk in the figure below.
In our model, there is a second, Antarctic polar cap that is not visible because of the curve
of the Earth.
After melting assume the water is evenly spread around the Earth.
The additional depth is small compared to the radius of the Earth. , and centered on the axis of rotation of the rest of the Earth.
Treat the rest of the Earth as a uniform sphere of mass and radius given in the table of constants.
An approximate representation of an Arctic polar cap of these dimensions is shown
as the unrealistically red disk in the figure below.
In our model, there is a second, Antarctic polar cap that is not visible because of the curve
of the Earth.
After melting assume the water is evenly spread around the Earth.
The additional depth is small compared to the radius of the Earth.
|
Table of Constants
Speed of Light (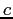 ) ) |
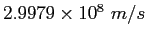 |
proton/neutron mass |
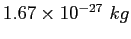 |
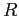 |
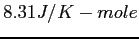 |
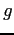 |
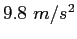 |
| Gravitation constant |
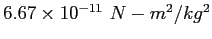 |
Electron mass |
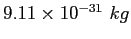 |
| Earth's mass |
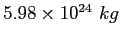 |
Earth's radius |
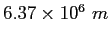 |
| Earth-Moon distance |
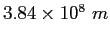 |
Earth-Sun distance |
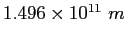 |
Table of Equations

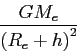
![\includegraphics[height=1.75in]{twod_collision_crasha.eps}](img72.png)
![\includegraphics[height=1.25in]{acceleration1.ps}](img73.png)
![\includegraphics[height=1.0in]{rocks.eps}](img74.png)

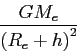
![\includegraphics[height=1.75in]{twod_collision_crasha.eps}](img72.png)
![\includegraphics[height=1.25in]{acceleration1.ps}](img73.png)
![\includegraphics[height=1.0in]{rocks.eps}](img74.png)
![\includegraphics[height=2.5in]{polarCap1.eps}](img40.png)
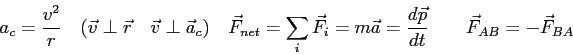
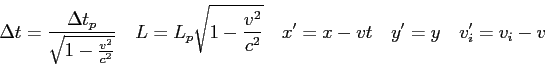
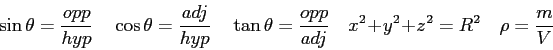

![\includegraphics[width=6.0in]{10t02a.ps}](img69.png)
![\includegraphics[width=6.0in]{10t02b.ps}](img70.png)