Physics 131-3 Final Exam

I pledge that I have neither given nor received unauthorized assistance during the completion of this work.

Signature height0pt depth1pt width3in

Questions (5 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

1. Consider two children playing catch in the aisle of a moving train. What is the difference in the flight of the ball, if any, between what a passenger on the train sees and what someone standing stationary on the ground observes?

2. A paradox is defined in the Merriam-Webster online dictionary as `an argument that apparently derives self-contradictory conclusions by valid deduction from acceptable premises'. What is paradoxical about the twins paradox?

3. Suppose Ashley and Ryan each throw darts at targets as shown below. Each of them is trying very hard to hit the bulls eye each time. Which one is better? Explain in terms of the average value and uncertainty of their hits.

   

4. Suppose you have a dynamics cart sitting on a track with a motion sensor at one end. The opposite end of the track is tilted upward. You give the cart a shove up the track, remove your hand, and start the motion sensor. Sketch the acceleration versus time graph you would observe until the cart comes to a stop. Explain your reasoning.

   

5. In the bottom panel of the figure below sketch the acceleration versus time graph that would match the velocity versus time plot that is shown in the top panel of the figure. State the reasoning behind your sketch.

   

6. Three uniform solids with identical masses are shown below (a square ring, a disk, and a circular ring). Which one has the greatest rotational inertia about an axis through its center of mass and perpendicular to its cross section? Which one has the least? Explain.

   

7. When an object moves in a full, circular path in a fixed amount of time, what quantity (other than time or mass) remains unchanged for circles of different radii? Explain.

8. A proton collides with a stationary nucleus in a one-dimensional collision. Consider the momentum versus time plots shown below. Are all of them physically possible? Explain.

   

9. In the figure below, a block is released from rest on a track with an initial potential energy $U_i$. The curved portions of the track are frictionless, but the horizontal portion of length $L$ produces a frictional force $f$ on the block. If $U_i = 2.25~fL$, then how trips does the block make across the horizontal section? Explain. Where does the block come to a halt? Explain.

   

10. A person riding a Ferris wheel at an amusement park moves through the positions at (a) the top, (b) the bottom, and (c) midheight. Rank the three positions according to the magnitude of the net centripetal force on the person. Explain your reasoning.

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1.	7 pts.	You wish to make a round trip from Earth in a spaceship traveling at constant speed in a straight line for 1 year and then returning at the same constant speed. You wish, further, on your return to find Earth as it will be 100 years in the future. How fast must you travel?
2.	7 pts.	A $3.0~kg$ block is dropped from a height of $0.30~m$ onto a spring of spring constant $k= 1800~N/m$. What is the maximum distance the spring is compressed?
3.	7 pts.	A high-speed railway car goes around a flat, horizontal circle of radius $R=500~m$ at a constant speed. The magnitudes of the horizontal and vertical components of the force of the car on a $60-kg$ passenger are $F_x = 239~N$ and $F_y = 588~N$, respectively. What is the magnitude of the net force (of all the forces) on the passenger? What is the speed of the car?

4.	7 pts.	In the 1968 Olympics in Mexico City, Bob Beamon shattered the world record for the long jump with a jump of $8.90~m$. Assume that his speed upon takeoff was $9.5~m/s$, about equal to that of a sprinter. The value of $g$ in Mexico city is $9.78~m/s^2$. His angle at takeoff was $45^\circ$. What is the expression for the maximum possible range in the absence of air resistance? How close did this world class athlete come to this maximum?
5.	7 pts.	Radioactive isotopes are now routinely used for a wide variety of biological, medical, and chemical tasks. To store these materials requires shielding to protect workers from different types of radiation. Shielding for one type of radiation, the emission of neutrons, works best if the neutrons lose a large fraction of their initial kinetic energy in colliding with the nuclei of the shielding material. Consider a neutron that scatters elastically through $180^\circ$ (a head-on collision) with the nucleus of a shielding atom. What is the ratio of the final kinetic to initial kinetic energy of the neutron? Get your answer in terms of the masses of the nuclei. Would heavy or light atomic nuclei make better shielding?
6.	7 pts.	For regulatory purposes the Bureau of Alcohol, Tobacco, and Firearms tests certain properties of firearms like muzzle speed. The speed of a bullet leaving a gun is hard to measure with cameras, radar guns, sonic rangers, etc. Consider the following method. A heavy, uniform rod of mass $m_r$ and length $l$ pivots about a point on one end $A$ and a heavy block of mass $m_b$ is attached to the other end. The rod-block combination hangs vertically with the block initially on the bottom as shown in the `before' part of the figure. A bullet of mass $m_g$ is fired horizontally into the block and the block, rod, and bullet swing upward to a maximum angle of $\theta$ (the `after' part of the figure). Treat the block and the bullet as point masses that are attached to the end of the rod. What is the expression for the minimum velocity of the bullet just before it hit the block?

Some Useful Constants

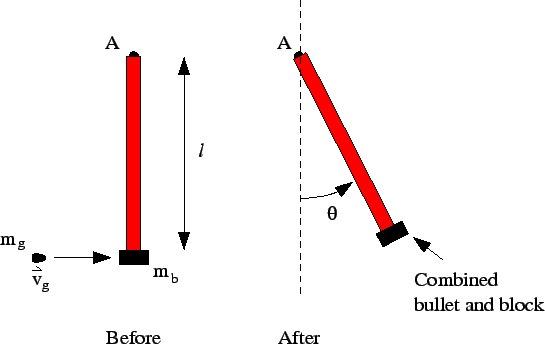
Acceleration of gravity ($g$)	$9.8~m/s^2$	Speed of light ($c$)	$2.9979\times 10^8~m/s$
Neutron mass	$1.68 \times 10^{-27}~kg$	Proton mass	$1.68 \times 10^{-27}~kg$
Earth mass	$5.98\times 10^{24}~kg$	Earth-Sun distance	$1.5\times 10^{11}~m$
Earth radius	$6.37\times 10^6~m$	atomic mass unit (u)	$1.66 \times 10^{-27}~kg$
1 day	$8.64\times 10^4 ~s$	1 year	$3.154 \times 10^7~s$
1 hour	$3600 ~s$	Sun mass	$1.99\times 10^{30}~kg$
1 mile	$1.610\times 10^3~m$	Gravitational constant	$6.67\times 10^{-11}~Nm^2/kg^2$
Speed of light (c)	$3.0\times 10^8~m/s$

Some Useful Equations

$$\Delta x = x_{finish} - x_{start} \qquad \Delta \vec r = \ve... ...{start} \quad \Delta \vec v = \vec v_{finish} - \vec v_{start}$$

$$\langle \vec v~ \rangle = {\Delta \vec r \over \Delta t} \qq... ...a t \to 0} {\vec r (t+\Delta t) - \vec r(t) \over \Delta t}$$

$$\langle \vec a \rangle = {\Delta \vec v \over \Delta t} \qqu... ...lta t \to 0} {\vec v(t+\Delta t) - \vec v(t) \over \Delta t}$$

$$\vec v = {d \vec r \over dt} = {dx \over dt}\hat i + {dy \... ...over dt}\hat i + {dv_y \over dt}\hat j + {dv_z \over dt}\hat k$$

$$x(t) = {1 \over 2}at^2 + v_0t + y_0 \quad v = at + v_0 \quad... ...er r} \quad ( \vec v \perp \vec r \quad \vec v \perp \vec a_c)$$

$$\vec F_{net} = \sum_i \vec F_i = m \vec a \qquad \vec F_{AB}... ...c = m {v^2 \over r} \quad F_s(x) = -kx \quad F_g(y) = mg \quad$$

$$W = \int \vec F \cdot d\vec s = \int F ~ds~ \cos\theta = ... ...v^2 \quad PE_s(x) = {1 \over 2} kx^2 \quad PE_g(y) = mgy \quad$$

$$E = KE + PE \quad ME_i = ME_f \quad \vec p = m \vec v \quad ... ... \quad \vec v_A = \vec v_B ~{\rm (perfectly\ inelastic)} \quad$$

$$(\vec J \quad or \quad \vec I) = \Delta \vec p = \int_{t_0... ...c F dt \qquad \vec r_{CM} = {\sum m_i \vec r_i \over \sum m_i}$$

$$\theta = {s \over r} \quad \omega = {v_T \over r} = {d\theta... ...t^2 + \omega_0 t + \theta_0 \quad \omega = \alpha t + \omega_0$$

$$KE = KE_t + KE_{rot} \quad KE_{rot} = {1\over 2}I_{cm}\omega... ...L = I \omega \quad \vec L_i = \vec L_f \quad v_{cm} = r\omega$$

$$\Delta t = {\Delta t_0 \over \sqrt {1 - {v^2 \over c^2}}} \q... ...^\prime = x - vt \quad y^\prime = y \quad v_i^\prime = v_i - v$$

$$\vec A = A_x \hat i + A_y \hat j + A_z \hat k \quad \vec A +... ... B = (A_x + B_x)\hat i + (A_y + B_y)\hat i + (A_z + B_z)\hat i$$

$$\vec A \cdot \vec B = A B \cos \theta \quad x = {-b \pm \sqr... ...} = 0 \quad {dt \over dt} = 1 \quad {dt^2 \over dt} = 2t \quad$$

$$\int f(x)dx = \lim_{\Delta x \rightarrow 0} \sum f(x_i) \D... ... x \qquad \int dx = x + c \qquad \int x dx = {x^2 \over 2} + c$$

$$\sin \theta = {opp \over hyp} \quad \cos \theta = {adj \over... ...quad \tan \theta = {opp \over adj} \quad x^2 + y^2 + z^2 = R^2$$

$$C = 2 \pi r \quad Area = \pi r^2 \quad Area = {1 \over 2}bh ... ...pi r^2 \quad V = {4 \over 3}\pi r^3 \quad V = \pi r^2 ~l \quad$$

$$\langle x \rangle = {\sum x_i \over N} \quad \sigma = \sqrt{ \sum (x_i - \langle x \rangle )^2 \over N-1}$$

Moments of Inertia