Physics 131-1 Test 3

I pledge that I have neither given nor received unauthorized assistance during the completion of this work.

Signature height0pt depth1pt width3in

Questions (10 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

1. University of Richmond President Bill Cooper stands on the Whitehurst clock tower and drops water balloons on passing students. His origin is the position of his hand when he drops the balloon. A student/target picks the ground to be the origin. They calculate different values for the mechanical energy before and after the water balloons are dropped. Why do they agree that the mechanical energy is conserved?

2. Suppose someone throws an egg at you and $\Delta t$ is the time you take to bring it to a halt as you catch it. To avoid breaking the egg should you catch the egg in such a way that $\Delta t$ is small or large? Why?

3. Consider the falling mass shown in the figure. Let the positive $y$ axis point down. Use the relationships between the linear and angular kinematic variables to derive the equation for the angular displacement $\theta$ from the equation below for $y$. Show all substitutions.
   
   $$y = y_0 + v_0 t + {1 \over 2} a t^2 \qquad .$$
   
   

   

4. Consider the situation shown in the figure. What is the magnitude and direction of the torque exerted by the force in terms of the quantities in the figure?

   

5. The figure below shows the $x-y$ trajectories of two objects that collide and stick together. Does the figure make sense? Why or why not?

   

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1.	15 pts.	A ball of mass $m=0.10~kg$ is thrown from a window with an initial velocity of $10.0~m/s$ at an angle of $45^\circ$ below the horizontal. Using energy methods, determine the speed of the ball when it is $4.0~m$ below the window.
2.	15 pts.	A 1500-kg car, heading north and moving at 40 miles per hour collides in a perfectly inelastic collision with a 5000-kg truck going east at 20 miles per hour. What is the velocity of the wrecked vehicles just after collision?
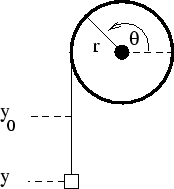
3.	20 pts.	Consider a rotating disk with a fixed axis of rotation at its center. It has a `rotational collision' with a cylindrical mass as shown in the figure. The disk has mass $m_d$, radius $r_d$, and it is initially rotating with angular velocity $\omega_0$. The cylinder has mass $m_c$, radius $r_c$, velocity $\vec v_c$, and lands and sticks with its center-of-mass at a point $r_1$ from the axis of rotation of the disk. The point of contact is the open circle on the disk in the figure. What is the final angular velocity of the disk and the weight? In what direction will the disk be rotating after the collision? =3.0in

Some constants and conversion factors.

Earth mass	$5.98\times 10^{24}~kg$	Earth-Sun distance	$1.5\times 10^{11}~m$
Earth radius	$6.37\times 10^6~m$	atomic mass unit (u)	$1.66 \times 10^{-27}~kg$
1 day	$8.64\times 10^4 ~s$	1 year	$3.154 \times 10^7~s$
1 hour	$3600 ~s$	Acceleration of gravity	$9.8~m/s$
1 mile	$1.610\times 10^3~m$