Physics 131-2 Final Exam

I pledge that I have neither given nor received unauthorized assistance during the completion of this work.

Signature height0pt depth1pt width3in

Questions (5 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

1. You are riding on a flat surface in a cart at a velocity $\vec v_{cart}$. You point a toy cannon up in the air at a $45^\circ$ angle and fire off a shot. How is the position that you measure for the horizontal position of the cannon ball related to the horizontal position a stationary observer would measure? A sketch might be useful here.

2. What would you see in a mirror if you carried it in your hands and ran at (or near) the speed of light? Explain.

3. Consider the one-dimensional position versus time plot below. Does the acceleration of the object change? If so, when is the acceleration largest and smallest? Explain.

   =3in

4. What is Roche's limit?

5. How does the vertical acceleration of a projectile on the Earth influence the horizontal acceleration? What is your evidence?

6. Three uniform solids with identical masses are shown below (a square ring, a disk, and a circular ring). Which one has the greatest rotational inertia about an axis through its center of mass and perpendicular to its cross section? Which one has the least? Explain.

   =3in

7. The figure below shows the $x-y$ trajectories of two objects that collide and stick together. Does the figure make sense? Why or why not?

   =1.7in

8. Consider the figure which shows force versus position. How would you determine the work done by the force? A sketch might be helpful here.

   =3.0in

9. Consider a simple pendulum (a mass on the end of a string) that is swinging back and forth. The forces on the suspended mass are gravity, the tension in the supporting string, and air resistance. Which of these forces, if any, do no work on the pendulum? Explain.

10. The Earth rotates about its axis and so is in a noninertial frame. Assuming the Earth is a uniform sphere would the apparent weight of an object (what you read off a scale) be the same at the equator and at the poles? Explain.

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1.	7 pts.	A spaceship, at rest in the reference frame $S$, is given a speed increment of $0.60c$. Relative to its new rest frame it is given a further $0.6c$ increment. This process is continued until its speed with respect to its original frame $S$ exceeds $0.99c$. How many increments does this process require?
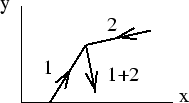
2.	7 pts.	A model rocket is fired vertically and ascends with a constant vertical acceleration of $3.0~m/s^2$ for $5.0~s$. Its fuel is then exhausted and it continues as a free-fall particle. What is the total elapsed time time from takeoff until the rocket strikes the Earth?
3.	7 pts.	The figure below shows what is known as a conical pendulum. The mass $m$, attached to a string, moves in a horizontal circle of radius $r$, with tangential velocity $v$. What is the angle $\theta$ that the string makes with the axis of the cone that the pendulum sweeps out. =1.7in
4.	7 pts.	A $1.0~kg$ block is dropped onto a vertical spring with spring constant $k=500.0~N/m$. The block becomes attached to the spring and the spring compresses $0.15~m$ before momentarily stopping. What is the speed of the block just before impact? =1.7in
		See next page.

5.	7 pts.	Show that if a neutron is scattered through $90^\circ$ in an elastic collision with a deuteron that is initially at rest, the neutron loses two-thirds of its initial kinetic energy to the deuteron. The mass of the neutron is $1.0~u$ and the mass of the deuteron is $2.0~u$.
6.	7 pts.	In 1992 telescope observations at the Smithsonian Astrophysical Observatory led astronomers to predict that comet Swift-Tuttle would collide with the Earth on August 14, 2126. Consider what will happen to the Earth if it collides with the asteroid and they stick together as shown in the figure. In this scenario the comet strikes the Earth at the equator with a velocity in the opposite direction to the Earth's rotation. The Earth is spinning about its axis as shown by the cross in the figure. Suppose the asteroid's speed is $9.0\times 10^5~ m/s$ in the center-of-mass (CM) reference frame. Remember that the net momentum in the CM frame is zero. The mass of the Earth is $6.0\times 10^{24}~ kg$ and the asteroid's mass is $8.0\times 10^{12}~ kg$. The asteroid's radius is $10^4~m$. The radius of the Earth is $6.4\times 10^6~m$. What would be the change in the angular velocity of the Earth-asteroid system after the collision? How much energy would be released in the collision? How does this amount of energy compare with the energy released by the atom bomb dropped on Hiroshima at the end of World War II? Is this event something to worry about? The Hiroshima bomb released $6.8\times 10^{13}~J$. =2.5in
7.	8 pts.	When large stars burn up all their nuclear fuel they can collapse into an object called a black hole which has so strong a gravitational field that even light cannot escape. Consider some of the difficulties associated with exploring such an object. The radius $R_h$ and mass $M_h$ of the black hole are related by $$R_h = {2GM_h \over c^2}$$ where $c$ is the speed of light and $G$ is the gravitational constant. Our intrepid astronaut is at a distance $r_0= 1.001R_h$ from the center of the black hole. If our astronaut is orbiting the black hole in a circular orbit, then what is the acceleration $a_g$ at $r_0$ in terms if $r_0$, $M_h$, $R_h$, and any other constants? What is $a_g$ if $M_h=3.2\times 10^{42}~kg$? If the astronaut is oriented so her feet are at $r_0$ and she is $1.8~m$ tall, is there a significance difference between the acceleration of her feet and the acceleration of her head? Will our intrepid astronaut stretch much?

Some Useful Constants

Acceleration of gravity ($g$)	$9.8~m/s^2$	Speed of light ($c$)	$2.9979\times 10^8~m/s$
Neutron mass	$1.68 \times 10^{-27}~kg$	Proton mass	$1.68 \times 10^{-27}~kg$
Earth mass	$5.98\times 10^{24}~kg$	Earth-Sun distance	$1.5\times 10^{11}~m$
Earth radius	$6.37\times 10^6~m$	atomic mass unit (u)	$1.66 \times 10^{-27}~kg$
1 day	$8.64\times 10^4 ~s$	1 year	$3.154 \times 10^7~s$
1 hour	$3600 ~s$	Sun mass	$1.99\times 10^{30}~kg$
1 mile	$1.610\times 10^3~m$	Gravitational constant	$6.67\times 10^{-11}~Nm^2/kg^2$