Physics 131-01 Test 3
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
- Suppose a ball of mass 0.20 kg is dropped and falls toward the surface of
the moon so that it hits the ground with a speed of 40 m/s and rebounds with
the same speed. Consider the ball and the moon as an interacting system with no other outside
forces. Why might the astronaut (who hasn't taken physics yet!) have the illusion
that momentum isn't conserved in the interaction between the ball and the moon?
- Using the diagram below, draw a dotted line in the direction you think your
two cars will move after a perfectly elastic collision between cars with different masses and
the same velocities.
Explain your reasoning in the space below.
![\includegraphics[width=1.5in]{fig1b.eps}](img53.png)
- Assume that an object is moving in a circle of constant radius,
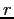 and recall that
and recall that 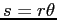 where
where
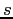 is the arc length along the edge of a circle,
is the arc length along the edge of a circle, 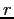 is the radius
of the circle, and
is the radius
of the circle, and  the angle.
Take the derivative of
the angle.
Take the derivative of 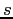 with respect to time to find the velocity of the object.
Show that the magnitude of the linear velocity,
with respect to time to find the velocity of the object.
Show that the magnitude of the linear velocity, 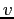 , is related to the magnitude of the angular velocity,
, is related to the magnitude of the angular velocity,
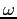 , by the equation
, by the equation 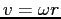 .
.
- Recall the laboratory where you studied a rotational collision. You dropped from rest a weight onto
a spinning rotator and measured the motion before and after dropping the weight from rest to test the
conservation of angular momentum.
Would the procedure you followed change if the weight was moving horizontally at a constant velocity
when you dropped it?
If it changed, what would be different?
- As global warming continues over the next century, some of the polar ice fields
will melt and more water will end up near the equator.
How would this change the moment of inertia of the Earth?
Would the length of a day increase or decrease?
Explain.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 2. |
20 pts. |
Measuring the moment of inertia of an irregularly-shaped object like the payload of a spacecraft
can be done with a device like the one shown in the figure.
A counterweight of mass  is suspended by a cord wound around a spool of radius is suspended by a cord wound around a spool of radius 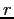 , forming part of a
turntable supporting the object.
The turntable can rotate without friction.
When the counterweight is released from rest, it descends a distance , forming part of a
turntable supporting the object.
The turntable can rotate without friction.
When the counterweight is released from rest, it descends a distance 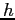 , acquiring a speed , acquiring a speed 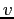 .
Show that the moment of inertia .
Show that the moment of inertia 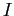 of the rotating apparatus including the turntable is of the rotating apparatus including the turntable is
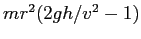 . .
|
| 3. |
25 pts. |
A widely accepted theory of planet formation states that planets form out of dust that collides and sticks to form larger and larger bodies.
When two of these `planetesimals' hit they can coalesce and form (through melting from the heat released in the collision) a single, spherical object.
A non-spinning planetesimal of mass  and radius and radius 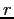 is moving with velocity is moving with velocity 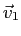 to the right as shown in the figure below.
It collides with an identical (same to the right as shown in the figure below.
It collides with an identical (same  and and 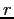 ), non-spinning planetesimal moving to the left with velocity ), non-spinning planetesimal moving to the left with velocity  and they stick together.
The velocities are parallel, but in opposite directions.
Their initial trajectories are a perpendicular distance and they stick together.
The velocities are parallel, but in opposite directions.
Their initial trajectories are a perpendicular distance 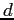 apart as shown in the figure.
They eventually form a uniform spherical body with mass apart as shown in the figure.
They eventually form a uniform spherical body with mass 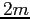 and radius and radius 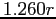 .
What is the velocity .
What is the velocity 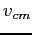 of the final object after the collision in terms of the information given above ( of the final object after the collision in terms of the information given above ( , , 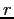 , , 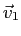 , ,  , and , and 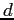 )?
What is its angular velocity )?
What is its angular velocity  after the collision in terms of the same information? after the collision in terms of the same information?
![\includegraphics[width=3.0in]{planetesimals1.eps}](img25.png)
|
Physics 131-1 Exam Sheet, Test 3
Speed of Light ( ) ) |
 |
proton/neutron mass |
 |
 |
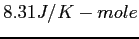 |
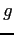 |
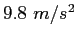 |
| Gravitation constant |
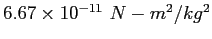 |
Earth's radius |
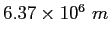 |
| Earth-Moon distance |
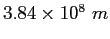 |
Electron mass |
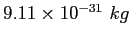 |
![\includegraphics[width=1.5in]{fig1b.eps}](img53.png)
![\includegraphics[width=1.5in]{fig1b.eps}](img53.png)
![\includegraphics[width=3.0in]{bullet2.eps}](img12.png)
![\includegraphics[width=2.5in]{fig2.ps}](img17.png)
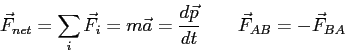
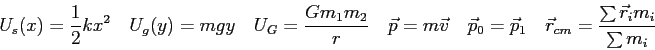
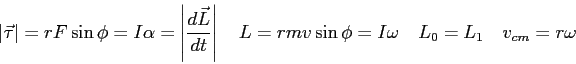
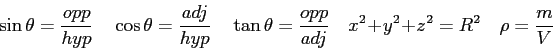
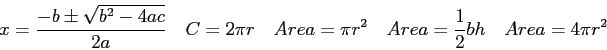
![\includegraphics[width=6.5in]{10t02a2.ps}](img51.png)
![\includegraphics[width=6.5in]{10t02b2.ps}](img52.png)