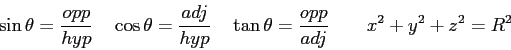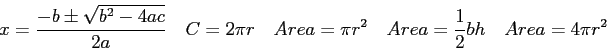Physics 131-01 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
- Newton's Third Law states that
 where the subscript
where the subscript  refers to
the force on object
refers to
the force on object 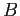 due to object
due to object 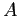 and
and 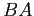 is the opposite. Why should you believe this? What is your evidence?
is the opposite. Why should you believe this? What is your evidence?
- A dynamics cart, pulley, hanging mass, and motion detector are set up as shown below.
Suppose you position the cart 0.10 m from the motion detector and give
it a push away from the motion detector and release it. Draw below vectors which
might represent the velocity, force and acceleration of the cart at each time
after it is released and is moving toward the right. Be sure to mark your arrows
with 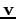 ,
,  , or
, or 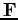 as appropriate.
Explain your reasoning.
as appropriate.
Explain your reasoning.
- Start with Newton's law of universal gravitation to show that the magnitude of the
acceleration due to gravity
on an object of mass
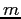 at a height
at a height  above the surface of the earth is given by the following
expression (
above the surface of the earth is given by the following
expression ( and
and 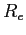 are the Earth's mass
and radius).
are the Earth's mass
and radius).

- In the Centripetal Force lab you extracted the centripetal force
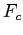 on the toy airplane
using the mass
on the toy airplane
using the mass 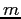 ,
average speed
,
average speed 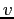 , radius
, radius 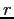 of the circular motion, and
of the circular motion, and 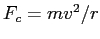 . You then determined the
angle
. You then determined the
angle 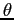 of the
string to the horizontal using
of the
string to the horizontal using 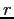 and
and 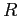 the
total length of the string that is actually rotating.
Now generate an expression for the vertical component
of the force exerted by the string. Make a vector diagram of the different components.
Generate an expression for the total force acting on the airplane.
the
total length of the string that is actually rotating.
Now generate an expression for the vertical component
of the force exerted by the string. Make a vector diagram of the different components.
Generate an expression for the total force acting on the airplane.
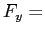
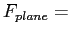
- When a particle moves from
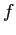 to
to  and from
and from  to
to  along the paths shown in the figure
and in the directions shown by the arrows along each trajectory, a conservative force
along the paths shown in the figure
and in the directions shown by the arrows along each trajectory, a conservative force 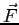 does the indicated amounts of work on it.
How much work is done by
does the indicated amounts of work on it.
How much work is done by 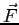 when the particle moves from
when the particle moves from 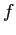 to
to  ? Explain.
? Explain.
![\includegraphics[height=1.25in]{f2.ps}](img66.png)
height0pt depth1pt width5.0in
Do not write below this line.
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
Physics 131-1 Exam Sheet, Test 2
Speed of Light (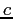 ) ) |
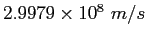 |
proton/neutron mass |
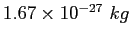 |
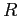 |
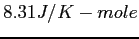 |
 |
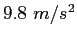 |
| Gravitation constant |
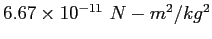 |
Earth's radius |
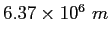 |
| Earth-Moon distance |
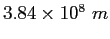 |
Earth mass |
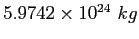 |
| Electron mass |
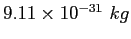 |
Moon mass |
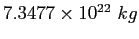 |
![\includegraphics[width=5.0in]{force2_fig2.eps}](img6.png)
![]() ,
, ![]() , or
, or ![]() as appropriate.
Explain your reasoning.
as appropriate.
Explain your reasoning.
![\includegraphics[width=5.0in]{force2_fig3.eps}](img10.png)
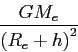

![\includegraphics[height=1.25in]{f2.ps}](img66.png)
![\includegraphics[width=1.5in]{prob1a.eps}](img38.png)
![\includegraphics[width=4.0in]{prob3.ps}](img39.png)