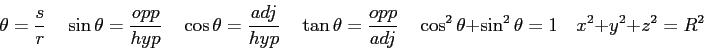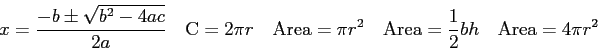Physics 131-01 Test 1


I pledge that I have neither given nor received unauthorized assistance during the completion of this work.


Signature height0pt depth1pt width3in


Questions (8 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.

  1. The velocity graph below shows the motion of two objects, A and B. Can you tell which object is ahead? Explain. Does either object reverse directions? Explain.


    \includegraphics[height=4.0cm]{f1.ps}

  2. The diagram below shows the positions of a cart at equal time intervals. (This is like taking snapshots of the cart at equal time intervals.) At each indicated time, sketch a vector above the cart which might represent the velocity of the cart at that time while it is moving toward the motion detector and speeding up.


    \includegraphics[height=2.0cm]{slowing_fig3.eps}

    Show below how you would find the vector representing the change in velocity between the times 1 s and 2 s in the diagram above. Based on the direction of this vector and the direction of the positive x-axis, what is the sign of the acceleration?

  3. Consider the histogram below of the measurements of the acceleration of gravity $g$. The average and standard deviation of the distribution are $11.0\pm 1.3 ~m/s^2$. What does the histogram of the class data tell you? Be quantitative in your answer. The accepted value is $g=9.8~m/s^2$.

    \includegraphics[height=3.0cm]{littleg1.eps}


  4. You are driving directly behind a pickup truck going at the same speed as the truck. A crate falls from the bed of the truck to the road. Will your car hit the crate before the crate hits the road if you neither brake or swerve? Explain.

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.

1. 8 pts. The position of a particle moving along the $x$ axis varies in time according to the expression

\begin{displaymath} x = At^2 + B \quad . \end{displaymath}

Evaluate the limit of $\Delta x /\Delta t$ as $\Delta t$ approaches zero. Do NOT use any derivative formulas for specific functions you might remember from calculus.


2. 15 pts. A particle starts from the origin and at rest and accelerates as shown in the red line in the figure. What is the particle's speed at $t=5~s$ and $t=15~s$. What is the distance traveled in the first $15~s$?


\includegraphics[width=2.5in]{graphs1.eps}

3. 20 pts. As their boosters separate, Space Shuttle astronauts typically feel accelerations up to $a=3.2g$ where $g=9.80~m/s^2$. In their training astronauts ride in a device where they experience such an acceleration as a centripetal acceleration. Specifically, the astronaut is fastened securely to the end of a mechanical arm which then turns at a constant speed in a horizontal circle. What is the rotation rate in revolutions per second required to give an astronaut a centripetal acceleration of $a=3.2g$ while in circular motion with radius $r = 10.0~m$?


4. 25 pts. In 1987 Natalya Lisovskaya of the former Soviet Union set the current world record in the shot put with a throw of $x_1 = 22.63~m$. The acceleration of gravity in Moscow is $9.8128~m/s^2$. If the event were held in Mexico City (site of the 1968 Olympics), her throw might have been significantly different because the acceleration of gravity there is only $g_M = 9.779~m/s^2$. What would have been the distance of her throw in Mexico City? Is the difference significant (i.e., for the shot put the difference must be bigger than a millimeter or $0.01~m$)? The initial velocity of the shot put is $v_0 = 14.305~m/s$ at a height $y_0 = 2.13~m$ above the ground and an angle of 45o to the horizontal.


Physics 131-01 Constants

Speed of Light ($c$) $2.9979\times 10^8~m/s$ proton/neutron mass $1.67\times 10^{-27}~kg$
$R$ $8.31J/K-mole$ $g$ $9.8~m/s^2$
Gravitation constant $6.67 \times 10^{-11}~N-m^2/kg^2$ Earth's radius $6.37\times 10^6~m$
Earth-Moon distance $3.84\times 10^8~m$ Electron mass $9.11\times 10^{-31}~kg$

Physics 131-01 Equations



\begin{displaymath} \Delta x = x_{finish} - x_{start} \qquad \Delta \vec r = \ve... ...{start} \quad \Delta \vec v = \vec v_{finish} - \vec v_{start} \end{displaymath}


\begin{displaymath} \bar v = \langle v \rangle = {\Delta x \over \Delta t} \quad... ...\to 0} {x (t+\Delta t) - x(t) \over \Delta t} = {dx \over dt} \end{displaymath}


\begin{displaymath} \bar a = \langle a \rangle = {\Delta v \over \Delta t} \quad... ... \to 0} {v(t+\Delta t) - v(t) \over \Delta t} = {dv \over dt} \end{displaymath}


\begin{displaymath} x = {1 \over 2}at^2 + v_0t + x_0 \qquad v = at + v_0 \qquad a_g = -g \end{displaymath}


\begin{displaymath} \vec A = A_x \hat i + A_y \hat j + A_z \hat k \quad \vec A +... ... B = (A_x + B_x)\hat i + (A_y + B_y)\hat i + (A_z + B_z)\hat i \end{displaymath}


\begin{displaymath} a_c = {v^2 \over r} \qquad \vec v \perp \vec r \qquad \vec v \perp \vec a_c \end{displaymath}


\begin{displaymath} \vec v = {d \vec r \over dt} = {dx \over dt}\hat i + {dy \... ...over dt}\hat i + {dv_y \over dt}\hat j + {dv_z \over dt}\hat k \end{displaymath}


\begin{displaymath} \theta = {s \over r}\quad \sin \theta = {opp \over hyp} \qua... ...uad \cos^2\theta + \sin^2\theta =1 \quad x^2 + y^2 + z^2 = R^2 \end{displaymath}


\begin{displaymath} x = {-b \pm \sqrt{b^2 -4ac} \over 2a} \quad {\rm C} = 2 \pi ... ... {\rm Area} = {1 \over 2}bh \quad {\rm Area} = 4 \pi r^2 \quad \end{displaymath}


\begin{displaymath} {\rm Volume} = {4 \over 3} \pi r^3 \qquad {\rm Volume} = \pi r^2 l \qquad \end{displaymath}