Physics 305 Test 2
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Instructions:
- This part of the exam is closed book, closed note.
- Please show your work. The grade you get depends on how well I can understand your solution even when you write down the correct answer.
- When I grade these problems, I typically give about 60-70% of the points for setting up a problem, and the rest for for doing the algebra, integrations,
derivatives, or whatever. Since time may be a factor, I recommend setting up all problems thoughtfully first, then going back to work out the messy stuff.
- If you can't remember something or need a hint to get started on a problem, I may be willing to trade hints for points off your grade. Make me an offer I can't refuse.
Multiple-Choice Questions (5 pts. apiece) Clearly circle the best answer among the different choices.
- A capacitor is constructed of two square metal plates of area
 separated
by a distance
separated
by a distance 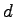 . One half of the space between the plates is filled with a substance of dielectric constant
. One half of the space between the plates is filled with a substance of dielectric constant  .
The other half is filled with another dielectric substance with constant
.
The other half is filled with another dielectric substance with constant 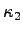 .
Calculate the capacitance of the device assuming the free space capacitance is
.
Calculate the capacitance of the device assuming the free space capacitance is 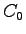 .
.
![\includegraphics[height=1.0in]{f1.eps}](img68.png)
- Use the fundamental concepts of electromagnetism to determine the electric field of an electric dipole
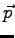 at a distance
at a distance
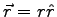 .
.
![\includegraphics[height=1.0in]{f2.eps}](img69.png)
- The electric potential of a grounded conducting sphere of radius
 in a uniform electric field is given as
in a uniform electric field is given as
![$\phi(r,\theta) = -E_0 r[1 - (a/r)^3]\cos\theta$](img19.png) . Find the surface charge distribution on the sphere.
. Find the surface charge distribution on the sphere.
![\includegraphics[height=0.9in]{f3.eps}](img70.png)
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
10 pts. |
A sphere of radius  , centered at the origin, carries charge density , centered at the origin, carries charge density
where  is a constant, and is a constant, and  , ,  , are the usual spherical coordinates. Find the approximate potential in the dipole approximation
for points on the , are the usual spherical coordinates. Find the approximate potential in the dipole approximation
for points on the 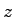 axis, far from the sphere. axis, far from the sphere. |
| 2. |
10 pts. |
A thick spherical shell (inner radius  , outer radius , outer radius 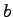 ) is made of dielectric material with a `frozen-in' polarization ) is made of dielectric material with a `frozen-in' polarization
where  is a constant and is a constant and 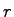 is the distance from the center (see figure).
There is no free charge in the problem.
Find the electric field in all three regions using the expression is the distance from the center (see figure).
There is no free charge in the problem.
Find the electric field in all three regions using the expression
to find 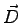 and then get and then get 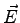 from the following. from the following.
![\includegraphics[height=1.5in]{f5.eps}](img44.png)
|
| 3. |
15 pts. |
Find an infinite series for the electric potential in the infinite slot shown below if the boundary at  consists
of two metal strips: one from consists
of two metal strips: one from  to to  , is held at a constant potential , is held at a constant potential 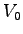 , and the other, from , and the other, from 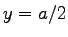 to to 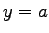 , is at potential , is at potential 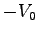 .
In other words, get the general solution for this problem and apply the boundary conditions to obtain
an infinite series for the electric potential with a single, unknown coefficient for each term in the series. You do NOT need to determine the unknown coefficient. .
In other words, get the general solution for this problem and apply the boundary conditions to obtain
an infinite series for the electric potential with a single, unknown coefficient for each term in the series. You do NOT need to determine the unknown coefficient.
|
Various and Sundry Equations and Constants
Speed of Light (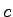 ) ) |
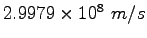 |
proton/neutron mass |
 |
 |
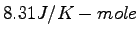 |
 |
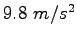 |
| Gravitation constant |
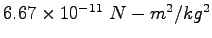 |
Earth's radius |
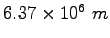 |
| Earth-Moon distance |
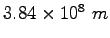 |
Electron mass |
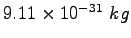 |
Physics Equations
![\includegraphics[height=1.0in]{f1.eps}](img68.png)
![\includegraphics[height=1.0in]{f2.eps}](img69.png)
![\includegraphics[height=0.9in]{f3.eps}](img70.png)
![\includegraphics[height=1.0in]{f1.eps}](img68.png)
![\includegraphics[height=1.0in]{f2.eps}](img69.png)
![\includegraphics[height=0.9in]{f3.eps}](img70.png)
![\includegraphics[height=1.1in]{f6.eps}](img43.png)
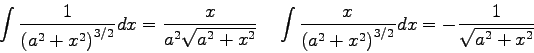
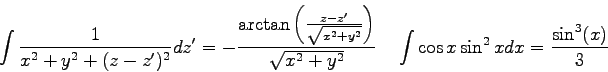
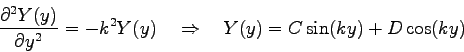


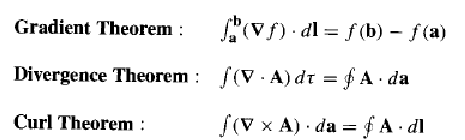
![\includegraphics[height=9.25in]{vectors1.ps}](img67.png)