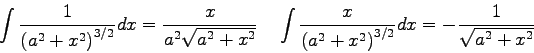Physics 305 Test 1
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Instructions:
- This part of the exam is closed book, closed note.
- Please show your work. The grade you get depends on how well I can understand your solution even when you write down the correct answer.
- When I grade these problems, I typically give about 60-70% of the points for setting up a problem, and the rest for for doing the algebra, integrations,
derivatives, or whatever. Since time may be a factor, I recommend setting up all problems thoughtfully first, then going back to work out the messy stuff.
- If you can't remember something or need a hint to get started on a problem, I may be willing to trade hints for points off your grade. Make me an offer I can't refuse.
Multiple-Choice Questions (5 pts. apiece) Clearly circle the best answer among the different choices.
- What defines a conservative force?
| A. |
 or or
 . . |
D. |
The force must be electromagnetic. |
| B. |
The force must be frictional. |
E. |
 or or
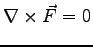 |
| C. |
The force must be nuclear. |
|
|
- Two infinite nonconducting sheets of charge are parallel to each other as shown in the figure.
Each sheet has a positive, uniform charge density
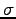 . Calculate the value of the electric field to the
right of the two sheets.
. Calculate the value of the electric field to the
right of the two sheets.
![\includegraphics[height=1.0in]{f1.eps}](img49.png)
- A thin rod stretches along the
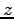 axis from
axis from 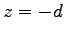 to
to  as shown.
Let
as shown.
Let 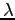 be the linear charge density or charge per unit length on the rod and the points
be the linear charge density or charge per unit length on the rod and the points
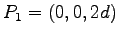 and
and 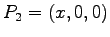 .
Find the coordinate
.
Find the coordinate  such that the potential at
such that the potential at 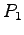 is equal to that at
is equal to that at 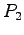 .
.
![\includegraphics[height=1.0in]{fig2.eps}](img50.png)
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
10 pts. |
Find the electric field (magnitude and direction) a distance 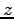 above the midpoint between two equal charges, above the midpoint between two equal charges, 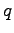 ,
a distance ,
a distance 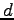 apart (see figure). Start from the field for a point charge. apart (see figure). Start from the field for a point charge.
![\includegraphics[height=1.0in]{fig3.eps}](img33.png)
|
| 2. |
10 pts. |
A charge 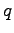 sits at the back corner of a cube of side sits at the back corner of a cube of side 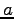 as shown in the figure.
What is the flux of as shown in the figure.
What is the flux of 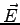 through the shaded side? In this problem get your solution to the point where
you have a well-defined integral to perform and STOP! Leave your answer in the form of this well-defined integral
in Cartesian coordinates. through the shaded side? In this problem get your solution to the point where
you have a well-defined integral to perform and STOP! Leave your answer in the form of this well-defined integral
in Cartesian coordinates.
![\includegraphics[height=1.75in]{fig4.ps}](img34.png)
|
| 3. |
15 pts. |
A hollow, spherical shell carries charge density
in the region 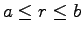 (see figure).
The electric field in the three regions is (see figure).
The electric field in the three regions is
where  is some constant and is some constant and  is the permittivity of free space.
Find the electric potential at the center of the shell using is the permittivity of free space.
Find the electric potential at the center of the shell using  at infinity as your reference point and starting from the definition
of the electric potential in terms of the electric field. at infinity as your reference point and starting from the definition
of the electric potential in terms of the electric field.
![\includegraphics[height=1.5in]{fig5.eps}](img35.png)
|
Various and Sundry Equations and Constants
Speed of Light (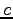 ) ) |
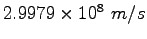 |
proton/neutron mass |
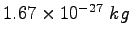 |
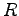 |
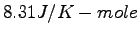 |
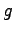 |
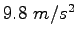 |
| Gravitation constant |
 |
Earth's radius |
 |
| Earth-Moon distance |
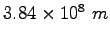 |
Electron mass |
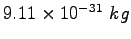 |
![\includegraphics[height=1.0in]{f1.eps}](img49.png)
![\includegraphics[height=1.0in]{fig2.eps}](img50.png)
![\includegraphics[height=1.0in]{f1.eps}](img49.png)
![\includegraphics[height=1.0in]{fig2.eps}](img50.png)