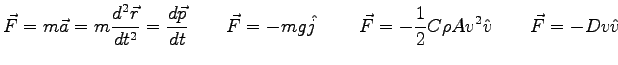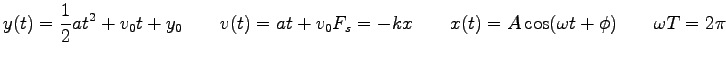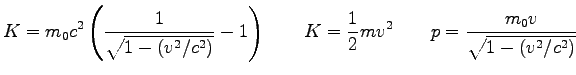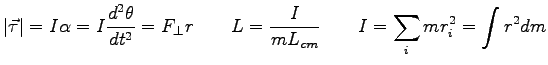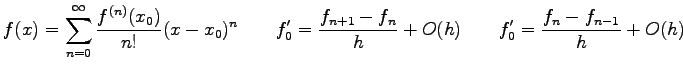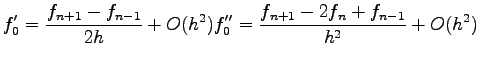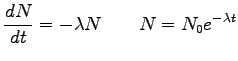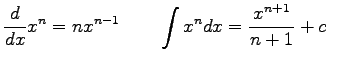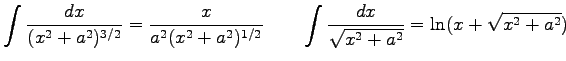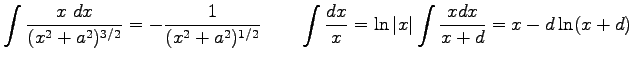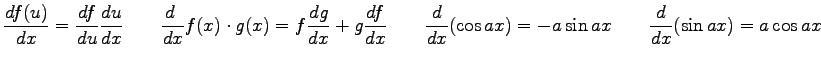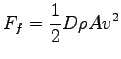
where
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
Problems. Work your solutions out on a separate piece of paper. Clearly show all work for full credit.
| 1. (10 pts.) |
The terminal speed of a skydiver in the spread-eagle position
is
|
| 2. (20 pts.) |
Provide an estimate to third order of the Fresnel integral. 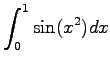
|
| 3. (20 pts.) | A body oscillates with simple harmonic motion according to the equation |
| 4. (20 pts.) |
The child/daughter nucleus formed in radioactive decay is often
radioactive itself.
Let
Where/When is the maximum value of |
|
Coulomb's Law constant (
|
|
Electron mass |
|
|
Elementary charge ( |
|
Proton/Neutron mass |
|
|
Permittivity constant (
|
|
|
|
|
|
|
|
|
|
|
|
Avogadro's number |
|