Physics 215 Midterm Exam, Spring, 2008
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- Which numerical method is better for calculating a first derivative,
the forward difference formula or the centered formula? Why?
- In lab, we numerically solved Newton's Second Law for a falling object (Lieutenant Chisov) in the form of a first-order ordinary
differential equation
where 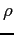 is the density of an object,
is the density of an object, 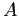 is the cross-sectional area,
is the cross-sectional area,
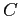 is the drag coefficient,
is the drag coefficient, 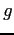 is the acceleration of gravity, and
is the acceleration of gravity, and 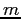 is the mass.
How do we use this solution to find how long the poor Lieutenant fell?
is the mass.
How do we use this solution to find how long the poor Lieutenant fell?
- Recall the differential equation for a physical pendulum which exhibited dynamical chaos
where 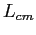 is the distance from the origin to the center-of-mass of the pendulum,
is the distance from the origin to the center-of-mass of the pendulum, 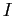 is the moment of inertia,
is the moment of inertia, 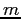 is the mass,
is the mass, 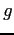 is the
acceleration of gravity,
is the
acceleration of gravity, 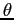 is the angular position of the pendulum,
is the angular position of the pendulum, 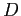 is the drag coefficient,
is the drag coefficient, 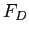 is the amplitude
of the driving force, and
is the amplitude
of the driving force, and 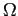 is the angular frequency of the driving force.
How would you extract the Poincare section from the solution to this differential equation?
What parameters in the differential equation might be useful?
is the angular frequency of the driving force.
How would you extract the Poincare section from the solution to this differential equation?
What parameters in the differential equation might be useful?
- What is the differential area in spherical coordinates that we used to develop an algorithm for choosing
a random direction? Use the figure below to clearly define the angles you are using.
![\includegraphics[width=2.0in]{f1.eps}](img59.png)
- We examined the problem of nuclear smuggling when we studied self-attenuation of radiation.
Why is this a problem especially in Russia?
- Consider the slab of material (dark green) shown in the figure which has density
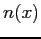 and
flux
and
flux
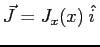 passing through it.
The width of the slab is
passing through it.
The width of the slab is 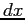 and the cross-sectional area is
and the cross-sectional area is 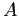 .
How is the amount of material in the slab related to
.
How is the amount of material in the slab related to 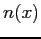 ?
How would you calculate the rate of change of the amount of material in the slab in terms of
?
How would you calculate the rate of change of the amount of material in the slab in terms of 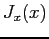 and parameters
like
and parameters
like  and
and 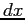 ?
?
![\includegraphics[width=2.25in]{f2.eps}](img60.png)
Problems. Work your solutions out on a separate piece of
paper.
Clearly
show all work for full credit.
| 1. (10 pts.) |
Consider the Taylor series
expansion of the exponential function 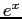 about the origin.
about the origin.
Show the expression above is correct.
|
| 2. (15 pts.) |
The variance 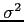 is the square of the standard deviation of a statistical distribution.
It is defined as
is the square of the standard deviation of a statistical distribution.
It is defined as
where the brackets mean the average value of the quantity.
Show the following.
Be sure to justify your steps.
|
| 3. (20 pts.) |
Consider the one-dimensional diffusion equation corresponding to particle in a long pipe
of length 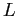
where 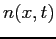 is the particle density,
is the particle density, 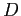 is the self-diffusion coefficient,
and
is the self-diffusion coefficient,
and 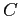 is the creation rate.
What is the dispersion relationship?
The solution to the diffusion equation can be found in the equation sheet.
is the creation rate.
What is the dispersion relationship?
The solution to the diffusion equation can be found in the equation sheet.
|
| 4. (25 pts.) |
Consider a baseball struck by Manny Ramirez and subject
to a friction force of the form
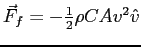 where
where 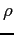 is the density,
is the density, 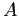 is the cross-sectional area,
is the cross-sectional area, 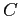 is the drag coefficient,
is the drag coefficient, 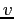 is the
velocity, and
is the
velocity, and  is a unit vector in the direction of the velocity.
is a unit vector in the direction of the velocity.
- What are the components of the total vector force on the object?
- Express your result from part 1 as a set of
first-order, linear, ordinary differential
equations where the components of the velocity vector are functions of
the time
 .
Be sure to express your answer in terms of the velocity components and any necessary constants.
.
Be sure to express your answer in terms of the velocity components and any necessary constants.
- Generate an algorithm to solve the equations from part 2
using the two-point formula for
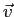 .
.
|
Constants and Equations
Coulomb's Law constant (
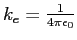 )
) |

|
Electron mass |
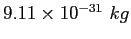
|
Elementary charge ( )
) |
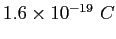
|
Proton/Neutron mass |
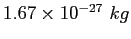
|
Permittivity constant (
 )
) |

|
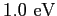
|
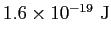
|
|
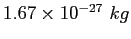
|
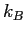
|
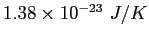
|
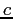
|
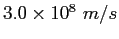
|
Avogadro's number |

|
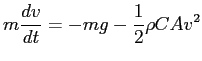
![\includegraphics[width=2.0in]{f1.eps}](img59.png)
![\includegraphics[width=2.25in]{f2.eps}](img60.png)
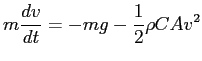
![\includegraphics[width=2.0in]{f1.eps}](img59.png)
![\includegraphics[width=2.25in]{f2.eps}](img60.png)
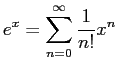
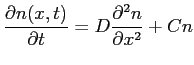
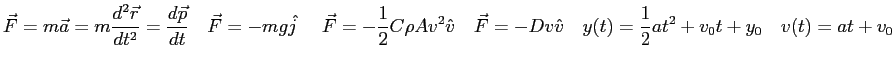
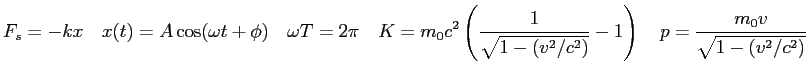
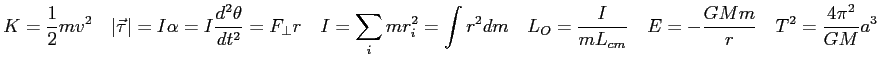
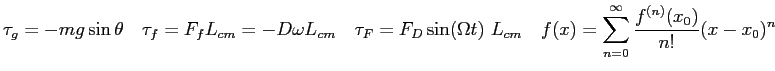
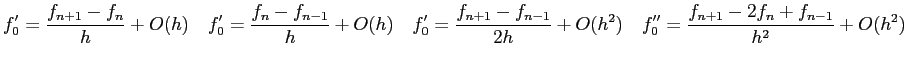

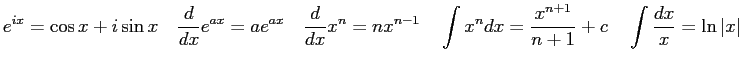
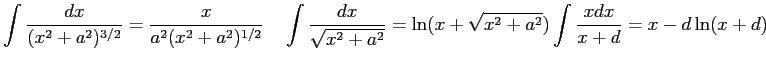

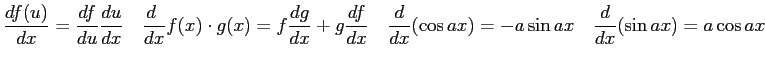
![\includegraphics[width=6.0in]{10t02a.ps}](img57.png)
![\includegraphics[width=6.0in]{10t02b.ps}](img58.png)