| A. | B. | ||
| C. |
|
D. |
|
| E. |
Assume that only the Coulomb force is important. The Li nucleus is accelerated to a kinetic energy of 50.0 MeV.
| A. | 1.12 fm | B. | 2.24 fm |
| C. | 3.54 fm | D. | 7.08 fm |
| E. | 8.20 fm |
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer questions 1-3 in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions 4-5 circle the correct answer.
| A. | B. | ||
| C. |
|
D. |
|
| E. |
| A. | 1.12 fm | B. | 2.24 fm |
| C. | 3.54 fm | D. | 7.08 fm |
| E. | 8.20 fm |
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 20 pts. | What is the distance of the center of mass of the earth-moon system from the center of the earth? |
| 2. | 25 pts. |
A proton of mass |
| 3. | 30 pts. |
In our study of Rutherford scattering we ignored the effect of the atomic electrons outside
the nucleus.
We now want to test that assumption.
Consider a gold target with |
Equations, Conversions, and Constants
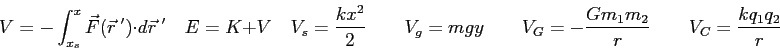
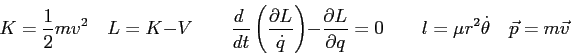
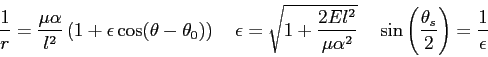
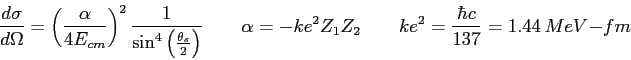
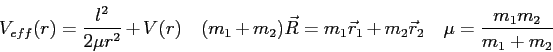
|
|
|
|
|
|
|
|
Speed of light ( |
|
|
|
|
|
|
|
|
|
|
|
|
Gravitation constant ( |
|
Earth's radius |
|
| Earth-Moon distance |
|
Moon's mass |
|
|
Coulomb constant ( |
|
Earth's mass |
|
|
Elementary charge ( |
|
Proton/Neutron mass |
|
|
Planck's constant ( |
|
Proton/Neutron mass |
|
|
Permittivity constant ( |
|
Electron mass |
|
|
Permeability constant ( |
|
Electron mass |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|