I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer in complete, well-written sentences WITHIN the spaces provided.
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work. See the next page for a table of equations and constants.
| 1. | 25 pts. |
A satellite is moving with a velocity
|
| 2. | 25 pts. |
Two atoms in a diatomic molecule with masses where
|
See next page.
| 3. | 30 pts. |
One of the early pictures of the atom was the Thomson
model.
The atom was viewed as a spherical cloud of uniformly
distributed positive charge and mass with a radius
of
|
Some useful constants and relationships.
|
|
|
|
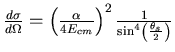 |
|
|
|
|
|
|
|
|
|