![\includegraphics[height=1.75in]{f1.eps}](img78.png)
| A. | 1.57 J | B. | 0.39 J |
| C. | 0.20 J | D. | 3.14 J |
| E. | 0.78 J |
A.
![]()
B.
![]()
C.
![]()
D.
![]()
E.
![]()

I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer questions 1-3 in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions 4-5 circle the correct answer.
![\includegraphics[height=1.75in]{f1.eps}](img78.png)
| A. | 1.57 J | B. | 0.39 J |
| C. | 0.20 J | D. | 3.14 J |
| E. | 0.78 J |
A.
![]()
B.
![]()
C.
![]()
D.
![]()
E.
![]()

Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 25 pts. |
For the damped oscillator the equation of motion is
where where 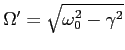 .
Apply the following boundary conditions .
Apply the following boundary conditions
|
|||
| 2. | 25 pts. |
A boat is slowed by a drag force where |
| 3. | 25 pts. |
A mass
|
Equations, Conversions, and Constants
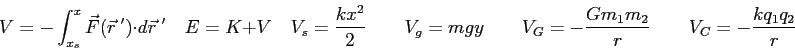
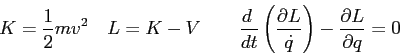
|
|
|
|
|
|
|
|
Speed of light ( |
|
|
|
|
|
|
|
|
|
|
|
|
Gravitation constant ( |
|
Earth's radius |
|
|
Coulomb constant ( |
|
Earth's mass |
|
|
Elementary charge ( |
|
Proton/Neutron mass |
|
|
Planck's constant ( |
|
Proton/Neutron mass |
|
|
Permittivity constant ( |
|
Electron mass |
|
|
Permeability constant ( |
|
Electron mass |
|
|
|
|
|
|