Physics 303 Test 1
I pledge that I have neither given nor received unauthorized
assistance
during the completion of this work.
Signature height0pt depth1pt width3in
Questions (5 pts. apiece) Answer in complete, well-written
sentences WITHIN the spaces provided.
- What is terminal velocity? Explain.
- What is the definition of the sine function in terms of
complex exponential functions?
- What is the difference between the motion of a `plucked', overdamped
oscillator and a `plucked',
underdamped oscillator?
- Consider the figure below which shows the potential energy
function for two charged particles.
Where are the turning points if the system has total energy
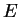 as shown with the dashed line?
Explain your choice graphically.
as shown with the dashed line?
Explain your choice graphically.
![\includegraphics[height=1.5in]{f1.eps}](img16.png)
Problems. Clearly show all reasoning for full credit.
Use a separate sheet to show your work.
| 1. |
25 pts. |
A bound particle of mass 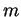 moves according to the potential energy moves according to the potential energy
where 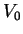 , ,  , and , and 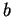 are positive.
Locate any equilibrium points and determine the spring
constant are positive.
Locate any equilibrium points and determine the spring
constant 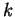 for small
oscillations about those equilibrium points.
Express your answer in terms of for small
oscillations about those equilibrium points.
Express your answer in terms of 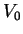 , ,  , and , and 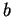 . . |
| 2. |
25 pts. |
An athlete can throw a javelin with an initial speed of 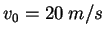 while standing still.
The horizontal ( while standing still.
The horizontal (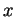 ) and vertical ( ) and vertical (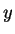 ) positions of the javelin are ) positions of the javelin are
where  is the initial angle of the javelin relative to the
horizontal.
Suppose the same athlete is now running at a speed of is the initial angle of the javelin relative to the
horizontal.
Suppose the same athlete is now running at a speed of 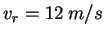 and throws the javelin with the same strength. and throws the javelin with the same strength.
- How would you modify the equations above to account for the
running motion of the athlete?
- At what angle should the athlete throw the javelin to get the
greatest
distance?
Use the results of part a to obtain your answer and assume the
the javelin is released from
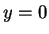 and returns to and returns to 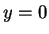 . .
|
| 3. |
30 pts. |
Consider the device shown below which could act as a filter to
remove pollutants from a liquid.
The filter consists of small elliptical holes that have beads of `active'
molecules
suspended in them that absorb specific chemicals from the liquid.
Two such beads are suspended in the filter's holes by using
short polymer chains that act as springs.
2.4in
- What is the Lagrangian for this system?
Only consider motion along the line of the `springs' (longitudinal motion)
and ignore the mass of the polymer chains.
- What are the equations of motion that describe the system?
- What are the eigenvalues or angular frequencies of the system?
![\includegraphics[]{f2.eps}](img15.png)
|
![\includegraphics[height=1.5in]{f1.eps}](img16.png)
![\includegraphics[height=1.5in]{f1.eps}](img16.png)