Physics 303
One-Dimensional Free Fall
- In solving Newton's Second Law for free fall through a resistive medium we used
the following expression to represent the drag force
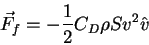 |
(1) |
where 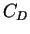 is the drag coefficient,
is the drag coefficient,
 is the density,
is the density, 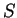 is the cross-sectional area,
is the cross-sectional area, 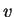 is velocity, and
is velocity, and 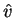 is
a unit vector in the direction of
is
a unit vector in the direction of 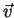 .
We found that
.
We found that 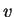 and
and 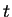 are related by
are related by
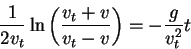 |
(2) |
where
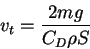 |
(3) |
and 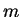 is the mass and
is the mass and 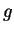 is the acceleration of gravity.
Show that Equation 2 can be written in the following form.
is the acceleration of gravity.
Show that Equation 2 can be written in the following form.
![\begin{displaymath}
v(t) = - v_t \left [ \frac{1 - \exp(-\frac{2gt}{v_t})}{1 + \exp(-\frac{2gt}{v_t})} \right ]
\end{displaymath}](img13.png) |
(4) |
- Show that Equation 4 can be written in the following form
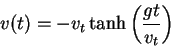 |
(5) |
where 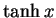 means the hyperbolic tangent of
means the hyperbolic tangent of 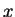 defined in the following way.
defined in the following way.
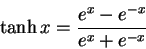 |
(6) |
- Apply a direct integration to Equation 5 to get the general solution for
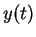 and then use the initial conditions that at
and then use the initial conditions that at  ,
, 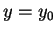 to find the
particular solution.
to find the
particular solution.
- Use the solution from Problem 3 to show that time it takes for Ms. Vulovic to
hit the ground can be written in the following way
![\begin{displaymath}
t_{hit} = \frac{v_t}{g} {\rm arccosh} \left [ \exp \left ( \frac{g y_0}{v_t^2} \right ) \right ]
\end{displaymath}](img21.png) |
(7) |
where
 means the inverse hyperbolic cosine of
means the inverse hyperbolic cosine of 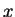 .
.
![\begin{displaymath}
v(t) = - v_t \left [ \frac{1 - \exp(-\frac{2gt}{v_t})}{1 + \exp(-\frac{2gt}{v_t})} \right ]
\end{displaymath}](img13.png)
![\begin{displaymath}
t_{hit} = \frac{v_t}{g} {\rm arccosh} \left [ \exp \left ( \frac{g y_0}{v_t^2} \right ) \right ]
\end{displaymath}](img21.png)
![\begin{displaymath}
v(t) = - v_t \left [ \frac{1 - \exp(-\frac{2gt}{v_t})}{1 + \exp(-\frac{2gt}{v_t})} \right ]
\end{displaymath}](img13.png)
![\begin{displaymath}
t_{hit} = \frac{v_t}{g} {\rm arccosh} \left [ \exp \left ( \frac{g y_0}{v_t^2} \right ) \right ]
\end{displaymath}](img21.png)