Animations of solutions to the Schrodinger equation

Traveling waves

Here is a solution to the Schrodinger equation for a free particle (that is, one with no forces acting on it, so the potential V = 0). This solution represents a wave traveling to the right. The red line is the absolute value of the wave function. The green curve is the real part, and the yellow curve is the imaginary part. Remember that the absolute value squared gives the probability. That is constant for this wave, which means that a particle with this wavefunction is equally likely to be anywhere.

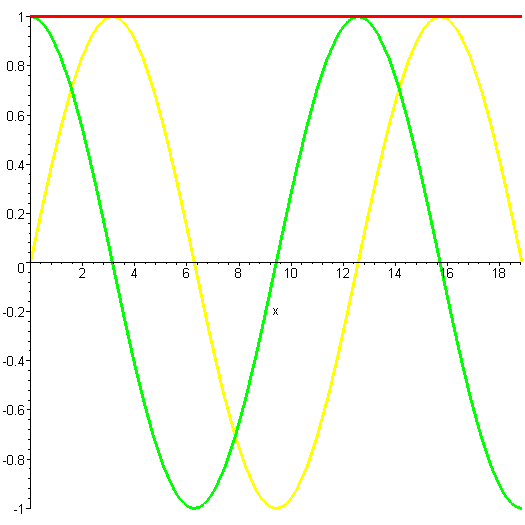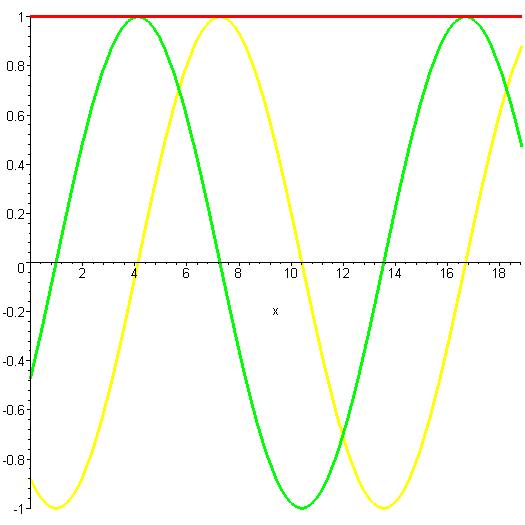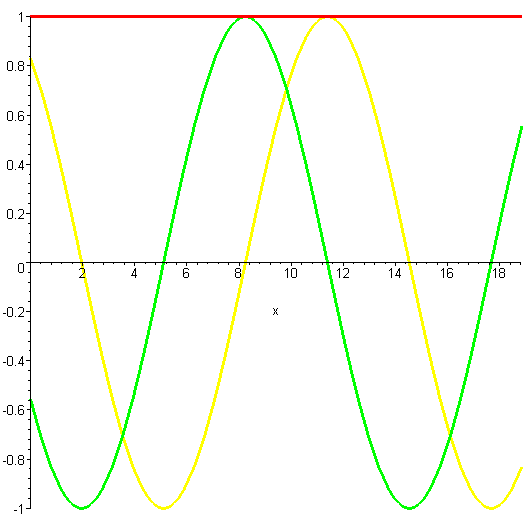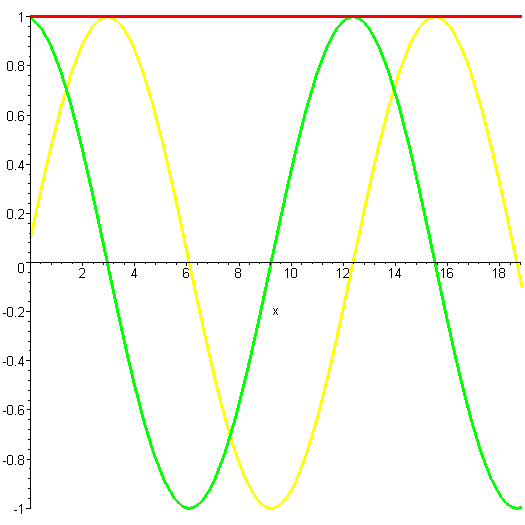
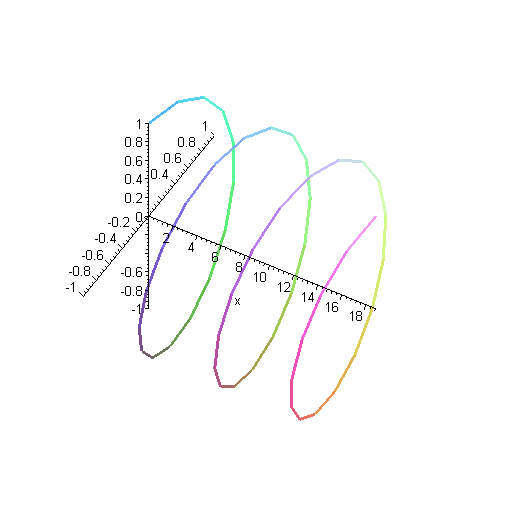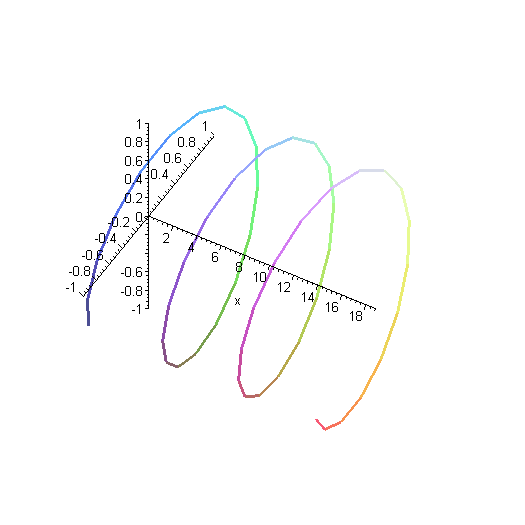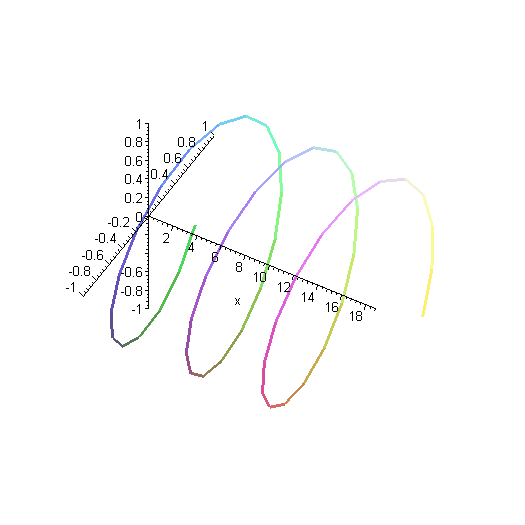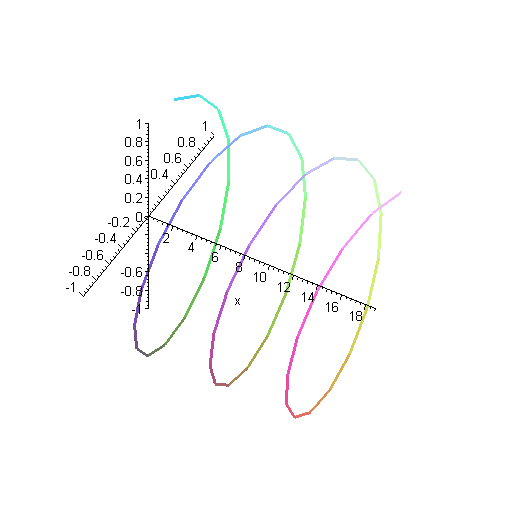
Here is another way of representing that solution. Instead of plotting the real and imaginary parts as separate curves, they're both plotted together. The y axis (the more horizontal-looking axis on the left) is the real part of the wavefunction, and the z axis (other axis on the left) is the imaginary part.

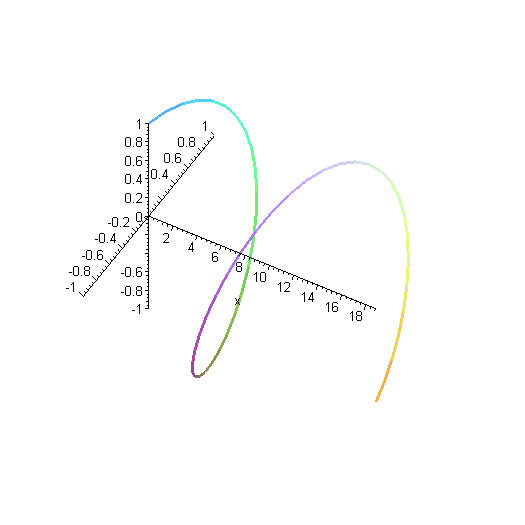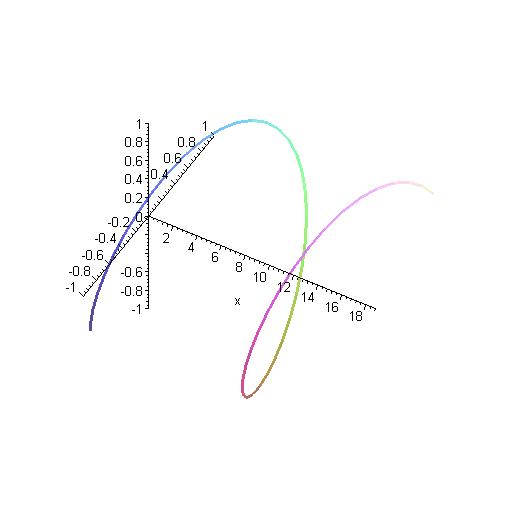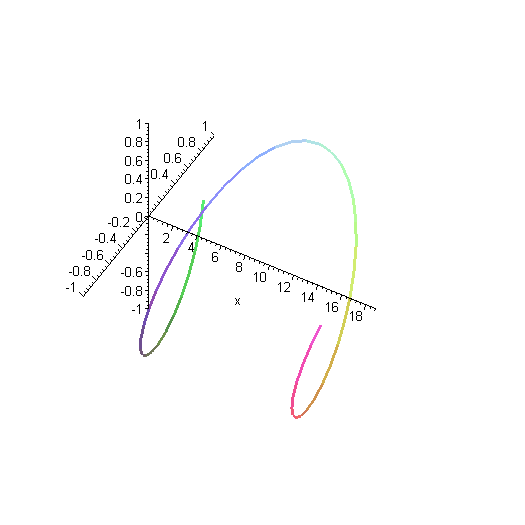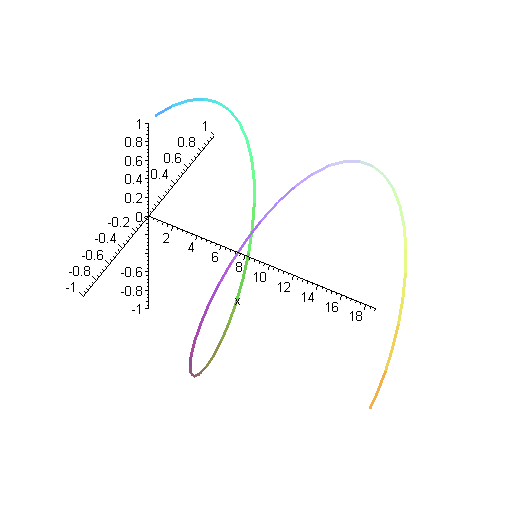
Remember as you look at this plot that the wavefunction really goes on forever in both directions, although we've only plotted a finite segment of it.

Here is another solution. This is a wave with twice as much momentum, as you can see by the shorter wavelength. That means it has four times as much kinetic energy. The higher energy is reflected in the fact that the wave oscillates more rapidly in time.

On the next page, we'll see some wave functions for particles in a square well.