Nodland & Ralston [1] claim to have discovered evidence for birefringence in the propagation of radio waves through the universe. We have argued [2] that flaws in their statistical analysis decrease the statistical significance of their results; Carroll & Field [3] reach similar conclusions. Further data from Leahy [4] and Wardle et al. [5] strongly argue against the proposed effect. In [6], Nodland & Ralston responded to our critique. Here, we explain why their response is incorrect.
Nodland & Ralston base their reply [6]
to our Comment on claims that
several of our assertions were in error. They raise a number of
different issues, but the chief arguments appear to fall into
three categories. They claim 1) that the distribution of the angle
used in their Monte Carlo methods differs from the uniform
distribution we ascribed to it, and 2) that one could measure a
birefringence even if the underlying angular distribution(s) were
uniform. They also claim 3) that our methods would obscure a
reasonable linear correlation even if it were in the data. We show
here in detail that they are in error in these three claims. Indeed,
we find nothing in their reply that gives us reason to modify our
Comment.
1) Nodland & Ralston object to our claim that the angle in
their simulations is drawn from a uniform distribution. We show here
that our assertion is correct, i.e. that the simulated 's
are indeed uniformly distributed.
The angle used in their statistical analysis does indeed depend on the
galaxy's position angle 
, its polarization angle 
,
its position on the sky, and the proposed birefringence direction
. However, the analysis procedure splits into two pieces: 1) the
determination of the angles 
and 
from and
, and 2) the choice of which of these angles to use given the
particular relative position of the galaxy and the birefringence
direction (i.e. in one half-space and in the
other). The search over many different , as detailed in their
procedures, never alters the values of or ; it
merely alters which one of them is used at any given time. Hence,
once and are determined from and
at the beginning of the calculation, one need never refer to
and again.
Moreover, the definitions of and reveal that
= 
. Hence, knowledge of for
each galaxy at the beginning of the calculation, before calculating
the correlation coefficient with respect to any birefringence direction,
is all the information needed about the galaxy's
polarization angles and position angles. This is true for both
of the Monte Carlo procedures described in [1].
Hence, to prove that our treatment is equivalent to theirs, all we need
do is show that drawing and from independent uniform
distributions yields a uniform distribution of . This is
fairly clear, but for completeness, we now show the algebra.
Assume that for a given galaxy the angles and are drawn
from independent uniform distributions on 
. Now, consider the
quantity 
. The probability density for this
quantity is obtained by convolving the uniform distributions of
and . The result is a triangle-shaped distribution,
for all values of 
between 
and 
.
(Here 
is an ordinary probability density: the probability
that lies between 
and 
is 
.)
Now apply equation (2) of [1] to convert to
. Given any between 0 and , there
are two values of that can correspond to this :
either 
or 
. Therefore, the
probability density for is
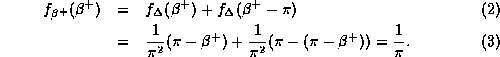
So is uniformly distributed on .
Hence, Nodland & Ralston's claim that our treatment differs from theirs is
incorrect.
Real radio galaxies do not have uniformly distributed values of
. This is clear from Figure 1d of [1], in which
is clearly seen to cluster around 
, and it is also
well known from previous studies of radio galaxies. Our argument is
that the incorrect assumption of uniformity artificially inflates the
statistical significance of their results.
Nodland & Ralston defend their procedure by pointing out that and
are uniformly distributed in the real data. That is correct but
irrelevant. Only differences between and enter the
calculation, and the correlation between the two angles causes
these differences (encoded in 
) to be distributed
nonuniformly. By drawing and from independent
uniform distributions, Nodland & Ralston fail to take this correlation
into account, leading to incorrect results.
2) Nodland & Ralston dispute our statement that ``if the underlying
galaxy population truly had a uniform distribution of , it
would be impossible to measure the proposed birefringence at all.''
To see why our statement is true, remember that one is trying to
measure an additional path-length-dependent variation on top of
the intrinsic angle between the polarization and the major axis. If
the polarization direction as the radiation left the galaxy were
unrelated to the galaxy position angle , one would never be able
to distinguish the initial polarization angle from the rotation induced
as the light traveled to us. Only by knowing something about the
relation between the intrinsic polarization direction and some other
observable property of the galaxy can one measure an additional
path-length-dependent rotation.
For a mathematical treatment of this, let us suppose for the moment
that the direction of the axis is fixed. Then as we have
argued, the Nodland-Ralston null hypothesis is equivalent to drawing
each value from a uniform distribution, generating ,
and then choosing the appropriate one according to the sign of
. Now, suppose that we ``rotate'' each in this
data set by adding (modulo ) the amount 
to each . Since the original
's were independently and uniformly distributed, the resulting
's will have precisely the same statistical distribution as
before: they will be independent and uniformly distributed. There is
therefore no statistical test that can distinguish between the
``rotated'' and ``unrotated'' data sets.
Nodland & Ralston propose as a counterexample a data set in which
there is a perfect linear relation between and 
.
While this data set has a uniform distribution of the observed
, it is not a case in which the underlying galaxy
population satisfies this uniform distribution, and hence it has no
bearing on the question at hand. Monte Carlo data sets drawn from
uniform intrinsic distributions of , with or without an
additional rotation, would have
a negligible probability to place all of the points so nicely on a
straight line. Since none of the Monte Carlo sets would look anything
like the data (as quantified, say, by the correlation coefficient),
this data would be not only striking evidence for birefringence
but also evidence against an uniform distribution of intrinsic
's. Indeed, it is exactly because the birefringent model
would reduce the distribution to a distance-independent
distribution that one favors this interpretation. Hence the
counterexample does not bear upon our claim, as it does not satisfy
the supposition of our assertion.
3) Nodland & Ralston claim that shuffling the data would fail to
detect a perfectly correlated 
distribution. This is
incorrect. Shuffling means randomly matching the x coordinate of
one data point with the y coordinate of another. If the data lay
on an inclined straight line, no permutations of the data would ever
produce a data set with as high a correlation; the new data sets would
generically show large amounts of scatter. In this particular
case, none of the shuffled data sets would have as high a
correlation as the original data, since the latter has the maximum
possible correlation coefficient (r=1).
Hence, the correlation would be detected at high significance.
In the latter half of their reply, Nodland & Ralston merely restate
our case. When they performed a somewhat more correct statistical
procedure (shuffling the 's), the statistical significance of
their result dropped considerably. They claim the signal is still
significant, but they do not account for the fact that one has looked at
many possible directions in the sky. In short, they confirm our
essential point that using the distribution of 's from the
observed distribution increases the correlation measured in the
non-refringent universe, thereby decreasing the statistical significance of
their claims. A similar calculation may be found in Carroll & Field
[3, p. 10].
In conclusion, we find that none of the arguments in [6] provide us with any reason to modify the conclusions of our original Comment.