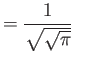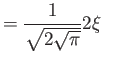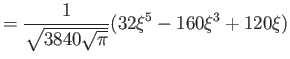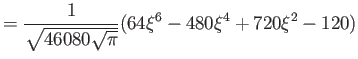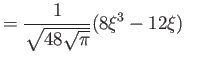Physics 309 Test 2
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature:
Questions (6 pts. apiece) Answer questions in complete, well-written
sentences WITHIN the spaces provided. For multiple-choice questions circle
the correct answer.
- What is the paradox of alpha decay?
- When we solved the harmonic oscillator Schroedinger equation with a power series, we
plugged the power series (
 ) into the differential equation and
gathered terms of like power and required the coefficient that multiplied
) into the differential equation and
gathered terms of like power and required the coefficient that multiplied 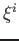 go to zero. Why?
go to zero. Why?
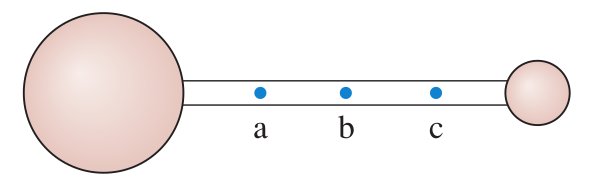
- The figure below shows the center-of-mass of the dumbbell at three
possible locations a, b, or c
with
 .
Which one is closest to the actual center-of-mass? Explain.
.
Which one is closest to the actual center-of-mass? Explain.
 (-156,20)
(-156,20) (-23,10)
(-23,10)
- The figures below show the change in the wave function for an initial square wave in
an infinite square well from
 to a later time.
Why does the square wave change so radically?
to a later time.
Why does the square wave change so radically?
- Consider the potential barrier shown below.
How would you use the transfer-matrix approach to connect the wave function
 in region 0
to the wave function
in region 0
to the wave function
 in region 4?
Give your answer in the appropriate notation used in class for the discontinuity and
propagation matrices.
What is the form of the wave number
in region 4?
Give your answer in the appropriate notation used in class for the discontinuity and
propagation matrices.
What is the form of the wave number  in each region?
in each region?
Problems. Work out your solutions on a separate sheet and clearly show all work for full credit.
| 1. (20 pts.) |
An electron beam (the electron mass is 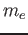 ) is sent through a rectangular potential barrier like the one in the figure of total length
) is sent through a rectangular potential barrier like the one in the figure of total length 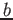 .
The transmission coefficient exhibits a second maximum at an energy
.
The transmission coefficient exhibits a second maximum at an energy 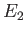 .
What is the barrier height in terms of
.
What is the barrier height in terms of 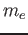 ,
, 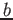 ,
, 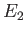 and any other constants?
and any other constants?
From our text we know the following.
|
| 2. (25 pts) |
The energy eigenvalues of a molecule indicate the molecule
is a one-dimensional harmonic oscillator.
In going from the second excited state to the first excited state, it
emits a photon of energy
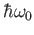 .
Assuming that the oscillating portion of the molecule is a proton of mass
.
Assuming that the oscillating portion of the molecule is a proton of mass 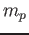 ,
calculate
the probability that a proton
in the first excited state is at a distance from the origin that
would be forbidden to it by classical mechanics.
You may have difficulty performing the integration necessary for the
final answer.
In that case, express your answer in terms of the
unsolved integral,
,
calculate
the probability that a proton
in the first excited state is at a distance from the origin that
would be forbidden to it by classical mechanics.
You may have difficulty performing the integration necessary for the
final answer.
In that case, express your answer in terms of the
unsolved integral, 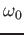 ,
, 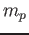 , and any other necessary constants.
You may find the table of equations helpful.
, and any other necessary constants.
You may find the table of equations helpful.
|
| 3. (25 pts.) |
Electrons of mass 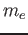 in a beam of density
in a beam of density 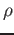 are accelerated through a voltage to obtain
an energy
are accelerated through a voltage to obtain
an energy 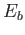 which `strikes' a potential step of height
which `strikes' a potential step of height 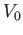 where
where
 as shown in the figure.
The beam is incident from the left so it's really `falling off' the barrier.
Starting from the general solution to the Schroedinger equation in each region in the figure,
what are the reflection coefficient and the reflected current (or flux) in terms of the parameters given above?
The eigenfunctions in each region are
as shown in the figure.
The beam is incident from the left so it's really `falling off' the barrier.
Starting from the general solution to the Schroedinger equation in each region in the figure,
what are the reflection coefficient and the reflected current (or flux) in terms of the parameters given above?
The eigenfunctions in each region are
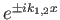 .
.
|
Do not write below this line.
width14cm height1pt depth0pt
Physics 309 Equations and Constants
The wave function,
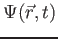 , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region 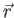 to
to
 .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
 and
and
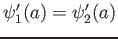 ) .
) .
Speed of light ( )
) |

|
fermi (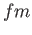 )
) |
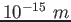
|
Boltzmann constant ( )
) |

|
angstrom (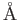 )
) |
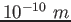
|
| |
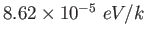
|
electron-volt ( )
) |
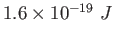
|
Planck constant (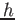 )
) |
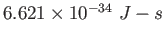
|
MeV |

|
| |

|
GeV |

|
Planck constant (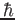 )
) |
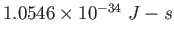
|
Electron charge (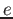 )
) |
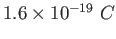
|
| |
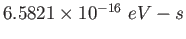
|
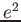
|

|
Planck constant ( )
) |

|
Electron mass (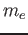 )
) |

|
| |
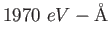
|
|
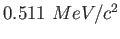
|
Proton mass (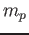 )
) |
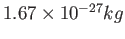
|
atomic mass unit (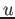 )
) |

|
| |

|
|

|
Neutron mass (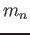 )
) |
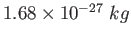
|
|
|
| |

|
|
|
Hermite polynomials ( )
)
 (-156,20)
(-156,20)![]() (-23,10)
(-23,10)![]()
 (-156,20)
(-156,20)![]() (-23,10)
(-23,10)![]()
![$\displaystyle T = \left [ 1 + \frac{1}{4}\frac{V^2}{E(E-V)} \sin^2 2 k_2 a\right ]^{-1} \quad E>V_0 \quad k_2 = \sqrt{\frac{2 m (E-V_0)}{\hbar^2}}
$](img13.png)
![$\displaystyle T = \left [ 1 + \frac{1}{4}\frac{V^2}{E(E-V)} \sinh^2 2 \kappa_2 a\right ]^{-1} \quad E<V_0 \quad \kappa_2 = \sqrt{\frac{2 m (V_0-E)}{\hbar^2}}
$](img14.png)
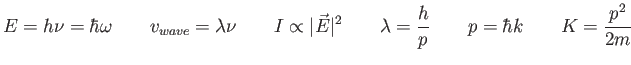




![]() , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region ![]() to
to
![]() .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
![]() and
and
![]() ) .
) .
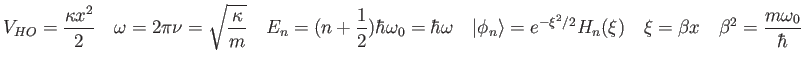
![$\displaystyle \psi_1 =
{\bf t} \psi_3 =
{\bf d_{12} p_2 d_{21} p_1^{-1}} \p...
...p\left [ -2 \int_{x_0}^{x_1}
\sqrt {2m(V(x) - E) \over \hbar^2} ~ dx\right ]
$](img36.png)

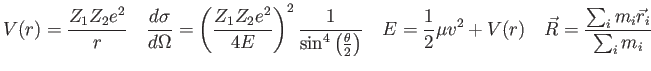


![$\displaystyle \frac{d}{dx}(\ln ax) = \frac{1}{x} \quad
\int x^n dx = \frac{x^{n...
...frac{1}{\sqrt{x^2 + a^2}} dx = \ln \left [ x + \sqrt{x^2 + a^2} \right ] \quad
$](img77.png)
![$\displaystyle \int \frac{x}{\sqrt{x^2 + a^2}} dx = \sqrt{x^2 + a^2} \quad
\int ...
...t{x^2 + a^2} - \frac{1}{2} a^2 \ln \left [ x + \sqrt{x^2 + a^2} \right ] \quad
$](img78.png)

![]() )
)