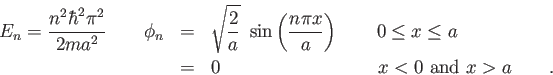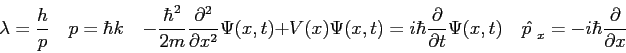Physics 309 Test 1
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (5 pts. apiece) Answer questions 1-4 in complete, well-written
sentences WITHIN the spaces provided. For multiple-choice question 5 circle
the correct answer.
- Cite two experimental results that show that energy can be quantized.
- What is the time-dependent solution
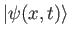 for a system with initial wave function
for a system with initial wave function
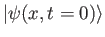 ,
eigenfunctions
,
eigenfunctions
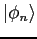 , and eigenvalues
, and eigenvalues 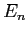 ? Your answer should be in terms of the knowns
? Your answer should be in terms of the knowns
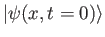 ,
,
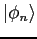 ,
, 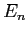 or other quantities you express in terms of those knowns.
or other quantities you express in terms of those knowns.
- The figure below shows evidence of the molar specific heat freeze out for diatomic molecules such as
 and
and 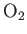 .
At low temperatures like
.
At low temperatures like 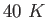 the molar specific heat of these molecules is the same as monatomic ones such as argon.
Explain why the molar specific heat rises from
the molar specific heat of these molecules is the same as monatomic ones such as argon.
Explain why the molar specific heat rises from 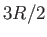 to
to 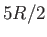 (where
(where 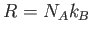 ,
, 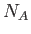 is Avogadro's number, and
is Avogadro's number, and 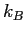 is Boltzmann's constant)
as the temperature rises to
is Boltzmann's constant)
as the temperature rises to 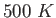 .
.
![\includegraphics[height=1.5in]{freezeout2.eps}](img73.png)
- Consider a particle-in-a-box in the following initial state
where the
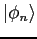 are the eigenfunctions for the states with energies
are the eigenfunctions for the states with energies 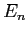 .
What is the probability of measuring
.
What is the probability of measuring 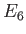 ?
?
- Which of the following is NOT a true statement about quantum
mechanics?
- The wave function is always a real quantity.
- The wave function represents the complete physical state.
- The quantities
 ,
, 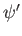 , and
, and
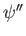 are finite, single-valued, and continuous.
are finite, single-valued, and continuous.
- For every observable, there is a quantum mechanical operator.
- In one dimension,
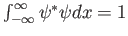 is required.
is required.
Problems. Clearly show all work for full credit. Use a separate sheet to show your work.
| 1. (15 pts) |
The work function of zinc is  .
What is the energy of the most energetic photoelectrons emitted by ultraviolet light of wavelength .
What is the energy of the most energetic photoelectrons emitted by ultraviolet light of wavelength
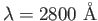 . .
|
| 2. (25 pts) |
What is the uncertainty relation for the product
 ? ?
|
| 3. (35 pts) |
Consider a case of one dimensional nuclear
`fusion'.
A neutron is in the potential well of a nucleus that we will
approximate with an infinite square well with
walls at 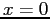 and and  .
The eigenfunctions and eigenvalues are .
The eigenfunctions and eigenvalues are
The neutron is in the  state when it fuses with another
nucleus that is the same size,
instantly putting the neutron in a new infinite square
well with walls at state when it fuses with another
nucleus that is the same size,
instantly putting the neutron in a new infinite square
well with walls at 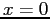 and and  .
(1) What are the new eigenfunctions and eigenvalues of the
fused system?
(2) Calculate the probabilities for finding the neutron in
the two lowest energy states of the fused system. .
(1) What are the new eigenfunctions and eigenvalues of the
fused system?
(2) Calculate the probabilities for finding the neutron in
the two lowest energy states of the fused system.
|
Physics 309 Equations, Conversions, and Constants
The wave function,
 , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region 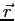 to
to
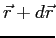 .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
Speed of light (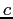 ) ) |
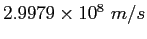 |
fermi (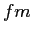 ) ) |
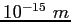 |
Boltzmann constant (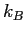 ) ) |
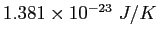 |
angstrom (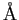 ) ) |
 |
| |
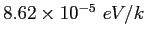 |
electron-volt (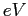 ) ) |
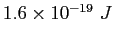 |
Planck constant ( ) ) |
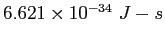 |
Neutron mass (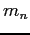 ) ) |
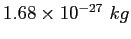 |
| |
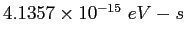 |
|
 |
Planck constant (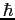 ) ) |
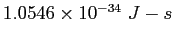 |
Electron charge (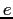 ) ) |
 |
| |
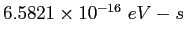 |
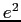 |
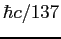 |
Planck constant (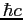 ) ) |
 |
Electron mass (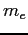 ) ) |
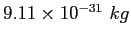 |
| |
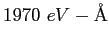 |
|
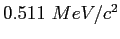 |
Proton mass (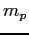 ) ) |
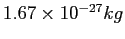 |
atomic mass unit (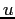 ) ) |
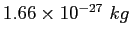 |
| |
 |
|
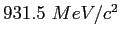 |
![\includegraphics[height=1.5in]{freezeout2.eps}](img73.png)
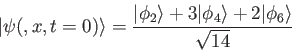
 ,
, 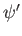 , and
, and
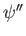 are finite, single-valued, and continuous.
are finite, single-valued, and continuous.
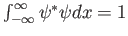 is required.
is required.