Physics 401 Test 1
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (5 pts. apiece) Answer questions 1-3 in complete, well-written
sentences WITHIN the spaces provided. For multiple-choice questions 4-5 circle
the correct answer.
- Cite at least two experimental results that motivated the development of quantum mechanics.
- What is the Rayleigh-Jeans Law (in words or equations)
and why was it important for the development of quantum mechanics?
- The eigenfunctions and eigenvalues of the particle
in a box are
for 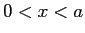 . The eigenfunctions are zero outside the box.
Consider the following sequence of measurements of a particle in a box.
. The eigenfunctions are zero outside the box.
Consider the following sequence of measurements of a particle in a box.
- The energy of the particle is measured. A value
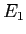 is obtained.
is obtained.
- The value of the position of the particle is made and a value
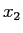 is obtained.
is obtained.
- The energy of the particle is measured again.
What possible values of energy can you obtain in step 3.c? Explain.
- What is the definition of a solid angle?
- We developed the Schroedinger equation by using a well-known classical physics
equation as a template and then adding in the Planck and de Broglie hypotheses.
What well-known classical equation did we use?
- When Fourier first introduced his ideas for expanding any function,
including those with `sharp' edges (recall the initial rectangular
wave packet we have seen in the computational
laboratory on superposition) the notion was met with some skepticism.
How would you convince someone that one can use the eigenfunctions of the
infinite square well to describe a rectangular wave?
Problems. Clearly show all work for full credit.
| 1. (15 pts.) |
An electron moves in the 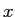 direction with the de Broglie wavelength direction with the de Broglie wavelength
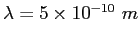 .
What is the energy of electron in eV?
What is the time-independent wave function of the electron? .
What is the energy of electron in eV?
What is the time-independent wave function of the electron?
|
| 2. (25 pts) |
What is the uncertainty relationship for
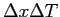 where where 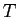 refers to the
kinetic energy operator refers to the
kinetic energy operator
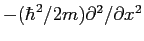 ? ?
|
| 3. (30 pts) |
The eigenfunctions and eigenvalues of the particle
in a box are
for 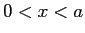 . The eigenfunctions are zero outside the box.
Measurement of the position of the a particle in a one-dimensional box
with walls at . The eigenfunctions are zero outside the box.
Measurement of the position of the a particle in a one-dimensional box
with walls at 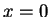 and and  finds the value finds the value  .
What is the probability for finding a particular energy value in a subsequent measurement?
What is the most probable value? .
What is the probability for finding a particular energy value in a subsequent measurement?
What is the most probable value?
|
Physics 401 Equations, Conversions, and Constants
Speed of light ( ) ) |
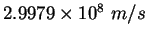 |
fermi ( ) ) |
 |
Boltzmann constant ( ) ) |
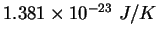 |
angstrom ( ) ) |
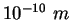 |
| |
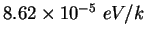 |
electron-volt (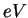 ) ) |
 |
Planck constant ( ) ) |
 |
MeV |
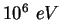 |
| |
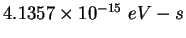 |
GeV |
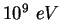 |
Planck constant ( ) ) |
 |
Electron charge (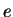 ) ) |
 |
| |
 |
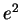 |
 |
Planck constant (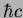 ) ) |
 |
Electron mass (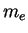 ) ) |
 |
| |
 |
|
 |
Proton mass (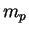 ) ) |
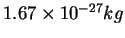 |
atomic mass unit (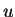 ) ) |
 |
| |
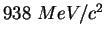 |
|
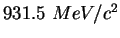 |
Neutron mass (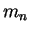 ) ) |
 |
|
|
| |
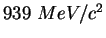 |
|
|
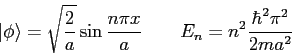
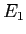 is obtained.
is obtained.
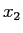 is obtained.
is obtained.

