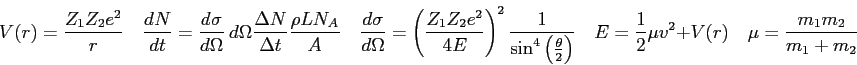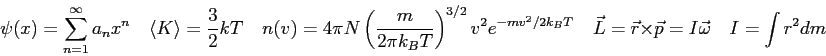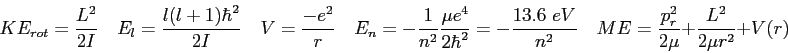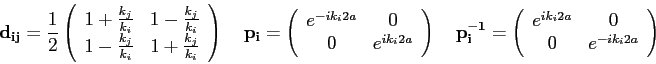Physics 309 Final, Fall 2014
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (3 pts. apiece) Answer questions in complete, well-written
sentences WITHIN the spaces provided. For multiple-choice questions circle
the correct answer.
- The hydrogen atom eigenfunctions can be represented as
 .
Describe the meaning of each quantum number.
.
Describe the meaning of each quantum number.
- Why did we use the center-of-mass coordinate system when we studied the
 molecule?
molecule?
- What is the quantum program?
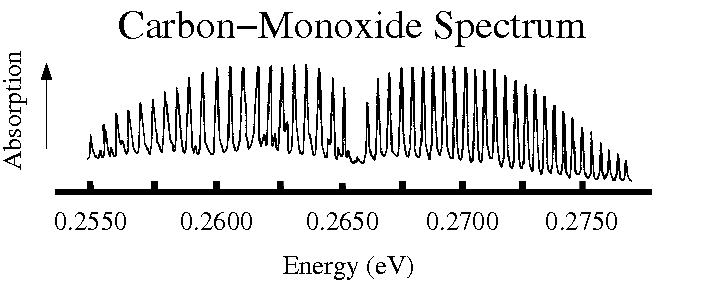
- Recall the absorption spectrum of carbon monoxide shown in the figure.
How would the spectrum change if the
 molecule did not rotate.
Explain.
molecule did not rotate.
Explain.
Do not write below this line.
- What is the definition of a solid angle?
- In solving the Schroedinger equation for the harmonic oscillator potential
we rewrote the Schroedinger equation in the form
where 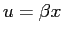 ,
, 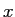 is the position of the particle, and
is the position of the particle, and 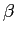 and
and 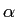 are constants.
What is the asymptotic form of this differential equation? Explain your reasoning.
are constants.
What is the asymptotic form of this differential equation? Explain your reasoning.
- A hydrogen atom is in the following initial state.
What is the value of the normalization constant? Show your reasoning for full credit.
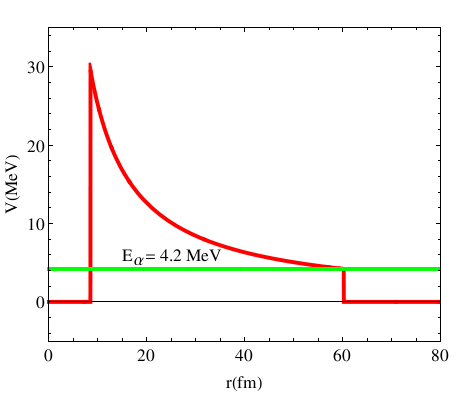
- The figure below shows the energy diagram we used to calculate alpha decay. What would
happen to the calculation of the lifetime if the energy
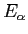 is increased?
Explain.
is increased?
Explain.
Do not write below this line.
- A particle in a box of width
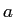 is in the initial state
is in the initial state
where
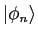 is the eigenfunction of the
is the eigenfunction of the 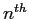 energy level.
The position of the particle is measured and a value
energy level.
The position of the particle is measured and a value 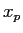 is found.
What would subsequent a subsequent measurement of the energy of the particle find?
Explain.
is found.
What would subsequent a subsequent measurement of the energy of the particle find?
Explain.
- A hydrogen atom is in its third excited state. What is the principle
quantum number
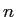 of the state it must jump to in order to absorb light with the
longest possible wavelength?
Explain.
of the state it must jump to in order to absorb light with the
longest possible wavelength?
Explain.
Problems. Put solutions on a separate piece of paper. Clearly show all work for full credit.
| 1. (11 pts.) |
The 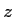 component of the angular momentum operator is component of the angular momentum operator is
We want to express this operator in terms of the spherical coordinates
 .
The transformation from Cartesian coordinates to spherical
coordinates is the following. .
The transformation from Cartesian coordinates to spherical
coordinates is the following.
Show
Hint: Use
 where where
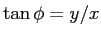 . .
|
| 2. (11 pts) |
With  in the recurrence relationship for the hydrogen atom in the recurrence relationship for the hydrogen atom
obtain 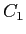 and use and use
to show
where 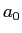 is the Bohr radius.
You do NOT have to calculate is the Bohr radius.
You do NOT have to calculate 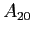 . .
|
| 3. (11 pts) |
The general solution to the classical harmonic oscillator is
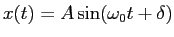 .
Starting from this equation get an expression for the period of the motion
(the time to make one complete oscillation) in terms of the
parameters of the general solution.
How is this result related to the frequency? .
Starting from this equation get an expression for the period of the motion
(the time to make one complete oscillation) in terms of the
parameters of the general solution.
How is this result related to the frequency? |
| 4. (11 pts) |
For the state
show that
If the parameter 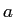 changes, then what happens to changes, then what happens to 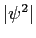 ? ?
|
| 5. (13 pts) |
Consider a case of one dimensional nuclear `fusion'.
A neutron is in the potential well of a nucleus that we will
approximate with an infinite square well with
walls at 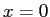 and and 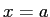 .
The eigenfunctions and eigenvalues are .
The eigenfunctions and eigenvalues are
The neutron is in the 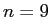 state when it fuses with another
nucleus that is twice its size,
instantly putting the neutron in a new infinite square
well with walls at state when it fuses with another
nucleus that is twice its size,
instantly putting the neutron in a new infinite square
well with walls at 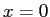 and and 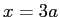 . .
See next page.
|
| 5. (cont.) |
- What are the new eigenfunctions and eigenvalues of the
fused system?
- Which state, if any, in the fused system will have the same energy
as the original state?
- Calculate the probabilities for finding the neutron in
the two lowest energy states of the fused system.
|
| 6. (13 pts) |
The general solution to the
rectangular barrier
problem for the potential shown in the figure is
where the wave numbers are defined as follows.
We expressed the wave functions in
each region in the form of column vectors
and the
boundary conditions in the form of the matrices
| | 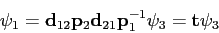 |
(1) |
where 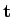 is the transfer matrix, is the transfer matrix,
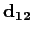 and and
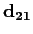 are discontinuity
matrices, and
are discontinuity
matrices, and  and and
 are the propagation
matrices.
The discontinuity and propagation matrices
are defined on the equation sheet.
Consider the elements of are the propagation
matrices.
The discontinuity and propagation matrices
are defined on the equation sheet.
Consider the elements of  , ,
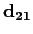 , ,
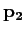 , and , and
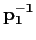 to be
known quantities.
In region 3 we set to be
known quantities.
In region 3 we set 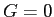 because no waves were incident from the right.
The coefficient because no waves were incident from the right.
The coefficient  represents the incident wave coming from the left.
It is our `beam' and so we consider it to be known. represents the incident wave coming from the left.
It is our `beam' and so we consider it to be known.
It turns out we can neglect the effect of the final
propagation matrix
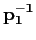 in Equation 1 for the calculation of
transmission and reflection coefficients.
The revised expression is the following. in Equation 1 for the calculation of
transmission and reflection coefficients.
The revised expression is the following.
| | 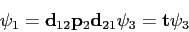 |
(2) |
Starting from Equation 2 above derive a relationship for the coefficient 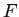 in terms of in terms of  and the
wave numbers and the
wave numbers 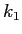 and and  .
Hint: Be judicious in your efforts.
You don't have to calculate every element of the transfer matrix. .
Hint: Be judicious in your efforts.
You don't have to calculate every element of the transfer matrix.
|
Physics 309 Equations
The wave function,
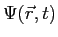 , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region 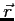 to
to
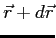 .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
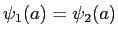 and
and
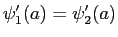 ) .
) .
Physics 309 Conversions, and Constants
Avogadro's Number (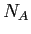 ) ) |
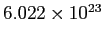 |
fermi (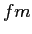 ) ) |
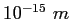 |
Boltzmann constant ( ) ) |
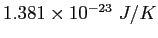 |
angstrom ( ) ) |
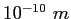 |
| |
 |
electron-volt (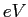 ) ) |
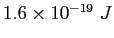 |
Planck constant (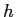 ) ) |
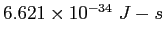 |
MeV |
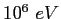 |
| |
 |
GeV |
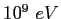 |
Planck constant (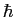 ) ) |
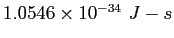 |
Electron charge (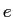 ) ) |
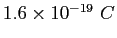 |
| |
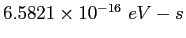 |
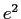 |
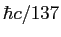 |
Planck constant (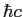 ) ) |
 |
Electron mass (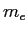 ) ) |
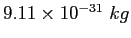 |
| |
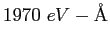 |
|
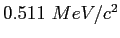 |
Proton mass (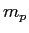 ) ) |
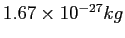 |
atomic mass unit (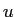 ) ) |
 |
| |
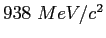 |
|
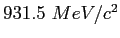 |
Neutron mass (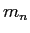 ) ) |
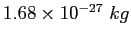 |
Speed of light (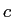 ) ) |
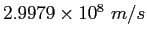 |
| |
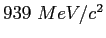 |
|
|
Transfer Matrices

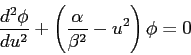

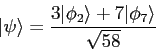

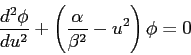

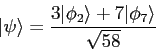
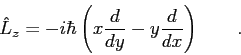
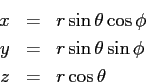
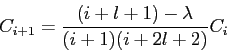
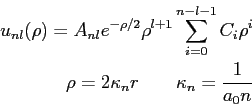
![\begin{displaymath}
\psi(x,t) = \frac{1}{\sqrt{a\sqrt{2\pi}}}\exp{\left [-\frac{...
...]}\exp{\left (\frac{ip_ox}{\hbar}\right )}\exp{(-i\omega_0 t)}
\end{displaymath}](img31.png)
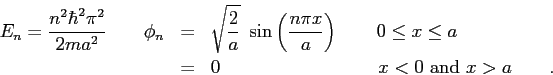
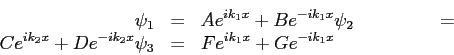
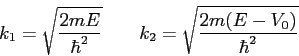
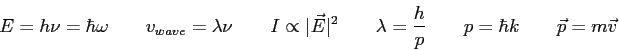

![\begin{displaymath}
\left [ \hat A,\hat B \right ] = \hat A \hat B - \hat B \hat...
...
(\Delta x)^2 = \langle x^2\rangle - \langle x\rangle^2 \qquad
\end{displaymath}](img65.png)
![]() , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region ![]() to
to
![]() .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued (
![]() and
and
![]() ) .
) .
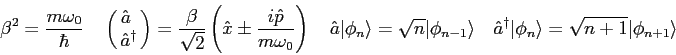
![\begin{displaymath}
\psi_1 =
{\bf t} \psi_3 =
{\bf d_{12} p_2 d_{21} p_1^{-1...
..._{x_0}^{x_1}
\sqrt {2m(V(x) - E) \over \hbar^2} ~ dx\right ]
\end{displaymath}](img73.png)