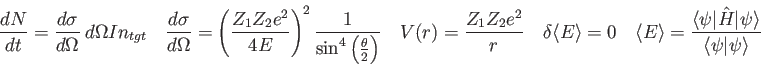Physics 309 Final
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Questions (3 pts. apiece) Answer questions in complete, well-written
sentences WITHIN the spaces provided. For multiple-choice questions circle
the correct answer.
- What is an absorption spectrum?
- In our model for the CO molecule what is the energy? Describe the components of your answer.
- Recall how the we explained the vibration-rotation
spectrum of the carbon monoxide molecule (see figure).
Suppose that when the molecule absorbed a photon
it was constrained to change the value of the angular
momentum quantum number by
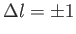 units AND
units AND
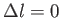 .
How would the spectrum change? Explain.
.
How would the spectrum change? Explain.
![\includegraphics[height=1.25in]{COspectrum3.eps}](img112.png)
- Why do we express the wave function in terms of energy eigenstates?
- Which of the following is NOT a
true statement about quantum physics?
A. The wave function is always a real
quantity.
B. The wave function represents the
complete physical state.
C. 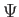 ,
,  , and
, and
 are finite, single-valued
and continuous.
are finite, single-valued
and continuous.
D. For every observable there is a quantum
mechanical operator.
- What is the value of the commutator
![$[\hat{H~},x]$](img6.png) for
the quantum mechanical Hamiltonian
for
the quantum mechanical Hamiltonian
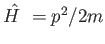 ?
?
- Two equal masses
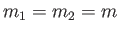 are connected by a spring
having Hooke's constant
are connected by a spring
having Hooke's constant 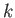 .
If the equilibrium separation is
.
If the equilibrium separation is 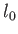 and the spring rests on a
frictionless horizontal surface, then what is the angular
frequency
and the spring rests on a
frictionless horizontal surface, then what is the angular
frequency 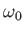 ?
?
- The figure shows the energy levels in eV for five different infinite potential wells trapping
a single electron in each.
The electron in well
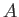 is excited to the fourth state at 25 eV and then de-excites by emitting
one of more photons corresponding to a single long jump or several smaller jumps.
There are no restrictions on the states that can be occupied.
What photon emission energies of the de-excitation of the electron in well
is excited to the fourth state at 25 eV and then de-excites by emitting
one of more photons corresponding to a single long jump or several smaller jumps.
There are no restrictions on the states that can be occupied.
What photon emission energies of the de-excitation of the electron in well 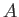 match
a photon absorption transition from the ground state for the other four wells (
match
a photon absorption transition from the ground state for the other four wells ( -
-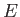 )?
Give the corresponding quantum numbers for the transitions in each well.
)?
Give the corresponding quantum numbers for the transitions in each well.
![\includegraphics[height=4.0cm]{question8.ps}](img113.png)
Problems. Clearly show all work for full credit.
| 1. (10 pts.) |
What is the uncertainty relationship for
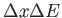 ?
Assume the problem is one dimensional. ?
Assume the problem is one dimensional.
|
| 2. (15 pts) |
Make the substitution 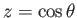 in the equation in the equation
and show that 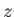 must satisfy Legendre's differential equation must satisfy Legendre's differential equation
|
| 3. (17 pts) |
The measured moment of inertia of the CO molecule is
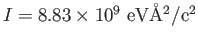 .
Using the definition of .
Using the definition of  and the fact that we are using the center-of-mass frame to
extract and the fact that we are using the center-of-mass frame to
extract  , calculate the separation of the two atoms in the molecule.
The mass of carbon is , calculate the separation of the two atoms in the molecule.
The mass of carbon is 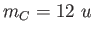 and the mass of oxygen is and the mass of oxygen is 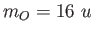 . .
|
| 4. (17 pts.) |
A 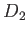 molecule is a rigid rotator at molecule is a rigid rotator at 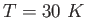 . At . At  it is in the state it is in the state
- a.
- What values of
 and and  will measurement find and what are their probabilities? will measurement find and what are their probabilities?
- b.
- What is
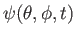 in terms of the moment of inertia in terms of the moment of inertia  and any other constants? and any other constants?
- c.
- What is
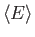 for the molecule at for the molecule at 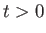 in terms of
the moment of inertia in terms of
the moment of inertia  and any other constants? and any other constants?
|
Continue 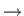
Problems (continued). Clearly show all work for full credit.
| 5. (17 pts) |
A molecule behaves like a one-dimensional harmonic oscillator.
In going from the third excited state to the second excited state, it
emits a photon of energy
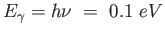 .
Assume the oscillating portion of the molecule is a proton ( .
Assume the oscillating portion of the molecule is a proton (
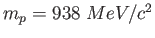 ). ).
- a.
- What is the maximum distance
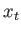 from the origin the proton will reach for a classical
oscillator? This is the turning point. Get your expression in terms of the total
classical energy of the oscillator. from the origin the proton will reach for a classical
oscillator? This is the turning point. Get your expression in terms of the total
classical energy of the oscillator.
- b.
- Now modify the result above for
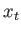 for a quantum mechanical oscillator in the for a quantum mechanical oscillator in the  state.
Get your answer in terms of state.
Get your answer in terms of 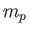 , , 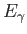 , and any other necessary constants. , and any other necessary constants.
- c.
- Now calculate the probability that a proton
in the second excited state is at a distance from the origin that
would be forbidden to it by classical mechanics.
Get your answer in terms of
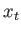 and and 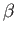 which is defined below along with the
wave function for the which is defined below along with the
wave function for the  state. state.
- d.
- Obtain a numerical value for
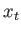 . .
Wave function and constants for the  harmonic oscillator state. harmonic oscillator state.
|
Physics 309 Equations
The wave function,
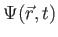 , contains all we know of a system and its
square is the probability of finding the system in the region
, contains all we know of a system and its
square is the probability of finding the system in the region 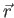 to
to
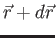 .
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
.
The wave function and its derivative are (1) finite, (2) continuous, and (3) single-valued.
width10cm height1pt depth0pt
Conversions and Constants
Speed of light (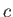 ) ) |
 |
fermi (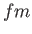 ) ) |
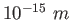 |
Boltzmann constant (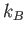 ) ) |
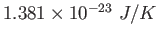 |
angstrom (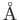 ) ) |
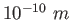 |
|
|
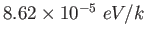 |
electron-volt (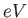 ) ) |
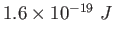 |
Planck constant (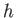 ) ) |
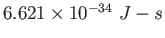 |
MeV |
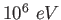 |
|
|
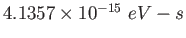 |
GeV |
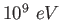 |
Planck constant (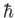 ) ) |
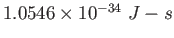 |
Electron charge ( ) ) |
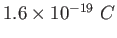 |
|
|
 |
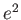 |
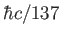 |
Planck constant (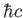 ) ) |
 |
Electron mass (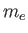 ) ) |
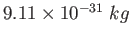 |
|
|
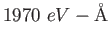 |
|
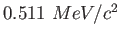 |
Proton mass (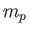 ) ) |
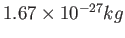 |
atomic mass unit (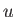 ) ) |
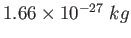 |
|
|
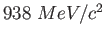 |
|
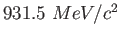 |
Neutron mass (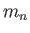 ) ) |
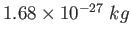 |
Avogadro's Number |
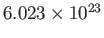 |
|
|
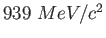 |
(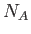 ) ) |
|
![\includegraphics[height=1.25in]{COspectrum3.eps}](img112.png)
![]() ,
, ![]() , and
, and
![]() are finite, single-valued
and continuous.
are finite, single-valued
and continuous.
![\includegraphics[height=4.0cm]{question8.ps}](img113.png)
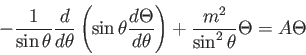
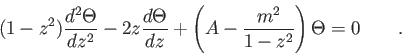
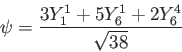
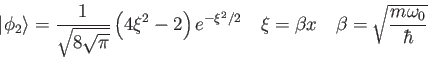
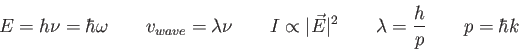
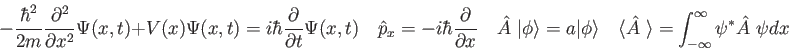
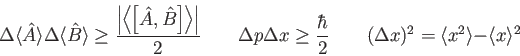
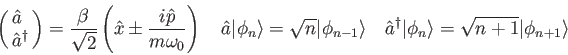
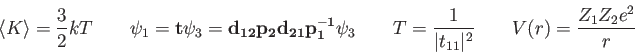
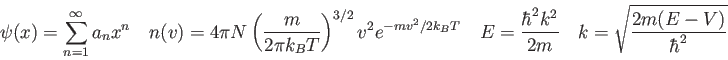
![\begin{displaymath}
\overline K = {3\over 2} kT \quad
\zeta_1 = {\bf t}\zeta_3 =...
..._{x_0}^{x_1}
\sqrt {2m(V(x) - E) \over \hbar^2} ~ dx\right ]
\end{displaymath}](img67.png)