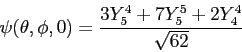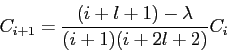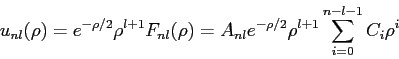Physics 402 Test 1
I pledge that I have given nor received unauthorized
assistance during the completion of this work.
Signature: width10cm height1pt depth0pt
Multiple Choice Questions (Circle your choice, 4 points apiece).
- Consider the hydrogen molecule
 as a rigid
diatomic rotor of separation
as a rigid
diatomic rotor of separation
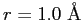 between two protons.
Calculate the energy of the
between two protons.
Calculate the energy of the  level in the rotational spectrum.
(
level in the rotational spectrum.
(
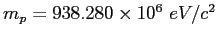 ,
,
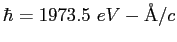 ).
).
| (a) |
0.10 eV |
(d) |
0.005 eV |
| (b) |
0.05 eV |
(e) |
0.10 eV |
| (c) |
0.15 eV |
|
|
- Calculate the
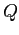 -value or energy release in MeV for the
nuclear reaction
-value or energy release in MeV for the
nuclear reaction
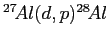 given that
given that
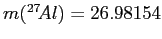 ,
,
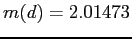 ,
,
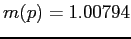 ,
and
,
and
 , all in
, all in 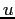 .
.
| (a) |
-6.32 MeV |
(d) |
6.83 MeV |
| (b) |
0.0 MeV |
(e) |
-6.83 MeV |
| (c) |
6.32 MeV |
|
|
- A simple wave function for the deuteron is given by
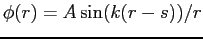 for
for
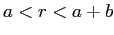 and
and
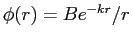 for
for
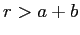 .
Find the probability that the neutron and the proton are
between
.
Find the probability that the neutron and the proton are
between  and
and 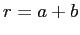 in separation.
in separation.
| (a) |
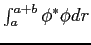 |
(d) |
 |
| (b) |
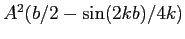 |
(e) |
1.0, since the proton and neutron are bound together |
| (c) |
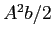 |
|
|
- The
 ,
,  hydrogen atom radial wave function is
hydrogen atom radial wave function is
What is the correct normalization factor  ?
?
Problems. Clearly show all work for full credit.
| 1. (20 pts.) |
A  molecule can be treated as a rigid rotator.
Consider a case where the molecule is at a temperature of molecule can be treated as a rigid rotator.
Consider a case where the molecule is at a temperature of 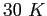 at at 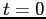 and in a state
and in a state
- (a)
- What are the possible values and associated probabilities for
a measurement of
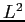 and and  ? ?
- (b)
- What is
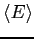 in terms of in terms of 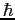 , the moment
of inertia , the moment
of inertia 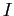 , and any other constants. , and any other constants.
|
| 2. (30 pts.) |
Consider the hydrogen atom eigenfunctions.
With 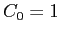 in the recurrence relationship in the recurrence relationship
obtain 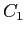 and and  for for  .
Then use the following expressions .
Then use the following expressions
to obtain 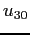 in terms of in terms of 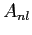 and and 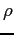 only.
Next, generate an
expression for only.
Next, generate an
expression for 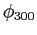 .
Do not worry about the normalization constant .
Do not worry about the normalization constant 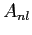 for for 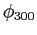 ;
just leave it as a constant. ;
just leave it as a constant.
|
| 3. (30 pts.) |
To derive the Coulomb part of the potential of an
atomic nucleus we assume the nuclear charge is uniformly distributed
throughout the volume of the nucleus.
We can apply Gauss' Law and obtain
where 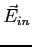 and and 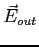 are the electric fields
inside and outside the nucleus respectively and are the electric fields
inside and outside the nucleus respectively and 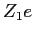 is the
charge of the nucleus.
Consider a point charge is the
charge of the nucleus.
Consider a point charge 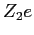 brought towards the first nucleus
so one can calculate the potential energy brought towards the first nucleus
so one can calculate the potential energy 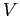 using the following definition. using the following definition.
Derive the form of the Coulomb part of the potential
inside and outside the nucleus.
|
Table of Constants
| Speed of light |
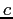 |
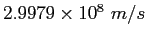 |
| Boltzmann's constant |
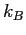 |
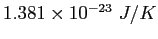 |
| |
|
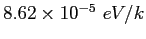 |
| Planck's constant |
 |
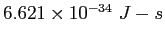 |
| |
|
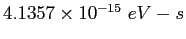 |
| |
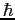 |
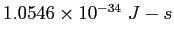 |
| |
|
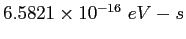 |
| |
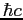 |
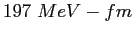 |
| |
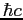 |
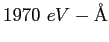 |
| Electron charge |
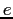 |
 |
| Electron mass |
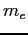 |
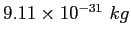 |
| |
|
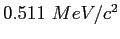 |
| Proton mass |
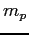 |
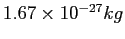 |
| |
|
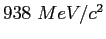 |
| Neutron mass |
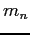 |
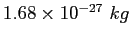 |
| |
|
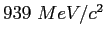 |
| atomic mass unit |
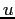 |
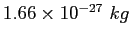 |
| |
|
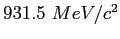 |
| Fine structure constant |
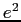 |
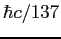 |