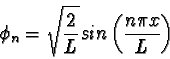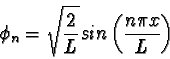Physics 309 Homework

Orthonormality

The wave functions that are solutions to the Schroedinger equation for a particle in an infinite square well potential are

$$\phi_n = \sqrt{2 \over L} sin \left ( {n\pi x \over L} \right )$$

where the walls of the `box' lie at x=0 and x=L.

1.

What are the energy eigenvalues and eigenfunctions of a particle in an infinite square well potential in terms of the mass of the particle, the size of the box, and any other physical constants?

2.

Show analytically that they comprise an orthonormal set of functions. It may be worthwhile to use the integrating power of Mathematica here. To obtain an indefinite integral of say sin² x use the following command: ``Integrate[ Sin[x]^ 2, x] ''. To find a definite integral for the same function over the range 0-2 use the following syntax: ``Integrate[ Sin[x]^ 2, $\{$ x, 0, 2 $\}$ ] ''.

3.

Once you have completed the analytical part of your argument use Mathematica to demonstrate visually the properties of the eigenfunctions that lead to this orthonormality. (Hint: What features of the integrand of the inner product between states with different values of the quantum number n imply the inner product is zero?)