![\includegraphics[height=1.5in]{vulovic1.eps}](img111.png)
For short distances
| A. |
|
B. |
|
| B. |
|
D. |
|
| C. |
|
| A. | 28.0 m/s | B. | 23.8 m/s |
| C. | 3.98 m/s | D. | 719 m/s |
| E. | 398 m/s |
![\includegraphics[height=1.0in]{ballisticPendulum.eps}](img112.png)
I pledge that I have neither given nor received unauthorized assistance during the completion of this work.
Signature height0pt depth1pt width3in
Questions (3 pts. apiece) Answer questions 1-6 in complete, well-written sentences WITHIN the spaces provided. For multiple-choice questions 7-8 circle the correct answer.
![\includegraphics[height=1.5in]{vulovic1.eps}](img111.png)
| A. |
|
B. |
|
| B. |
|
D. |
|
| C. |
|
| A. | 28.0 m/s | B. | 23.8 m/s |
| C. | 3.98 m/s | D. | 719 m/s |
| E. | 398 m/s |
![\includegraphics[height=1.0in]{ballisticPendulum.eps}](img112.png)
Problems. Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 1. | 12 pts. |
A particle moves subject to the potential energy
where |
Problems (continued). Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 2. | 12 pts. |
Two masses |
| 3. | 12 pts. |
Two particles on a line are mutually attracted by a force
where |
| 4. | 12 pts. |
Show the drag force on a satellite moving with velocity |
| 5. | 14 pts. |
In August 2004, observations of the star
![\includegraphics[height=2.8in]{phot-25d-04-normal.eps}](img38.png)
|
Problems (continued). Clearly show all reasoning for full credit. Use a separate sheet to show your work.
| 6. | 14 pts. |
Recall the way we used the conservation of energy in analyzing Rutherford scattering.
We started with the following form of the energy equation
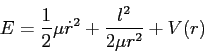
where where
|
Equations
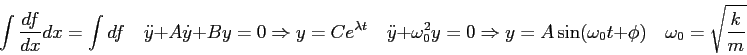

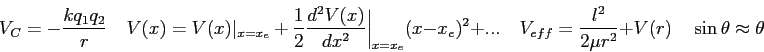
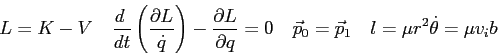

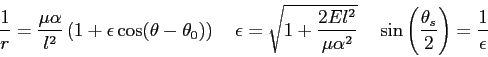
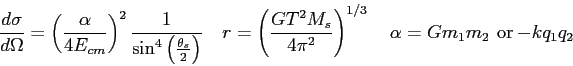
Constants and conversion factors
|
|
|
|
|
|
|
|
Speed of light ( |
|
|
|
|
|
|
|
|
|
|
|
|
Gravitation constant ( |
|
Earth's radius |
|
More constants and conversion factors
| Earth-Moon distance |
|
Moon's mass |
|
| Earth-Sun distance |
|
Earth's mass |
|
|
Coulomb constant ( |
|
Jupiter's mass |
|
|
Elementary charge ( |
|
Proton/Neutron mass |
|
|
Planck's constant ( |
|
Planck's constant ( |
|
|
Planck constant ( |
|
Planck's constant ( |
|
|
Planck's constant ( |
|
Planck's constant ( |
|
|
Permittivity constant ( |
|
Electron mass |
|
|
Permeability constant ( |
|
Electron mass |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|